题目内容
若函数f(x)满足f(2x)=x,则f(4)= ,f(6)= .
考点:函数的值
专题:函数的性质及应用
分析:换元法可得f(x)=log2x,代值计算即可.
解答:
解:令2x=t,则x=log2t,
∴f(t)=log2t,
∴f(x)=log2x,
∴f(4)=log24=2,
f(6)=log26=1+log23
故答案为:2;1+log23
∴f(t)=log2t,
∴f(x)=log2x,
∴f(4)=log24=2,
f(6)=log26=1+log23
故答案为:2;1+log23
点评:本题考查函数的值的求解,涉及换元法求函数的解析式,属基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
下列结论错误的是( )
| A、命题:“若a>b>0,则a2>b2”的逆命题是假命题 | ||||||||
| B、若函数f(x)可导,则f′(x0)是x0为函数极值点的必要不充分条件 | ||||||||
C、向量
| ||||||||
| D、命题p:“?x∈R,ex≥x+1”的否定是“?x∈R,ex<x+1” |
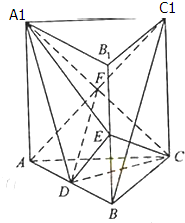 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4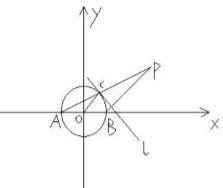 已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.
已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.