题目内容
已知函数f（x）=|x-2|+ax有最小值，求实数a的取值范围．
考点：函数的值域
专题：函数的性质及应用
分析：首先去掉绝对值，再讨论函数的增减性，根据增减性求出a的取值范围．
解答：
解：∵f（x）=|x-2|+ax
∴f(x)=
，
函数f（x）=|x-2|+ax有最小值，
则函数在x＜2时，为减函数，在x≥2时为增函数或常数函数．
即a-1≤0，且a+1≥0，
∴实数a的取值范围[-1，1]
∴f(x)=
|
函数f（x）=|x-2|+ax有最小值，
则函数在x＜2时，为减函数，在x≥2时为增函数或常数函数．
即a-1≤0，且a+1≥0，
∴实数a的取值范围[-1，1]
点评：本题主要考查了函数的增减性和最值的问题，属于基础题．
练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中，点M是AA1的中点，CM和DB1所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
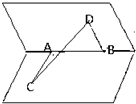二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的量两个半平面内，且都垂直于AB．已知AB=4，AC=6，BD=8，CD=2