题目内容
15.已知集合A={x|ax2+2x+a=0,a∈R},若集合A有且仅有2个子集,则实数a的取值组成的集合为( )| A. | {-1,0} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
分析 若A有且仅有两个子集,则A为单元素集,所以关于x的方程ax2+2x+a=0恰有一个实数解,分类讨论能求出实数a的取值范围.
解答 解:由题意可得,集合A为单元素集,
(1)当a=0时,A={x|2x=0}={0},此时集合A的两个子集是{0},∅,
(2)当a≠0时 则△=4-4a2=0解得a=±1,
当a=1时,集合A的两个子集是{1},∅,
当a=-1,此时集合A的两个子集是{-1},∅.
综上所述,a的取值为-1,0,1.
故选:D.
点评 本题考查根据子集与真子集的概念,解题时要认真审题,注意分析法、讨论法和等价转化法的合理运用.属于基础题.

练习册系列答案
相关题目
10.已知x0是函数f(x)=3x+$\frac{2}{1-x}$的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)>0,f(x2)>0 |
7.已知函数y=2cosx的定义域为[$\frac{π}{3}$,$\frac{4π}{3}$],值域为[a,b],则b-a的值是( )
| A. | 2 | B. | 3 | C. | $\sqrt{3}$+2 | D. | $2\sqrt{3}$ |
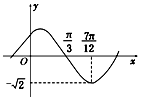 (1)求$f(x)=tan(3x-\frac{π}{4})$的定义域
(1)求$f(x)=tan(3x-\frac{π}{4})$的定义域