题目内容
已知m=(1,-
),n=(sin2x,cos2x),定义函数f(x)=m•n.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)已知△ABC中,三边a,b,c所对的角分别为A,B,C,f(
)=0.
(i)若acosB+bcosA=csinC,求角B的大小;
(ii)记g(λ)=|
+λ
|,若|
|=|
|=3,试求g(λ)的最小值.
| 3 |
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)已知△ABC中,三边a,b,c所对的角分别为A,B,C,f(
| A |
| 2 |
(i)若acosB+bcosA=csinC,求角B的大小;
(ii)记g(λ)=|
| AB |
| AC |
| AB |
| AC |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的求值,平面向量及应用
分析:(I)利用数量积运算、两角和差的正弦公式、正弦函数的单调性即可得出;
(II)由f(
)=0,代入可得A=
.
(i)由于acosB+bcosA=csinC,利用正弦定理可化为sinC=sinCsinC.由于sinC≠0,可得C=
.再利用三角形的内角和定理可得B=π-A-C.
(ii)利用数量积的性质和二次函数的单调性即可得出.
(II)由f(
| A |
| 2 |
| π |
| 3 |
(i)由于acosB+bcosA=csinC,利用正弦定理可化为sinC=sinCsinC.由于sinC≠0,可得C=
| π |
| 2 |
(ii)利用数量积的性质和二次函数的单调性即可得出.
解答:
解:(I)f(x)=
•
=sin2x-
cos2x=2(
sin2x-
cos2x)=2sin(2x-
),由-
+2kπ≤2x-
≤
+2kπ解得-
+kπ≤x≤
+kπ,k∈Z.
∴函数f(x)的单调递增区间为[-
+kπ,
+kπ](k∈Z);
(II)由f(
)=0,得2sin(A-
)=0,∵0<A<π,∴A=
.
(i)∵acosB+bcosA=csinC,利用正弦定理可得sinAcosB+sinBcosA=sinCsinC,化为sin(A+B)=sinCsinC,即sinC=sinCsinC,∵0<C<π,∴sinC≠0.
∴sinC=1,∴C=
.∴B=π-A-C=
.(ii)|
+λ
|=
=
,又|
|=|
|,A=
.∴|
+λ
|=
=3
,当λ=-
时,g(λ)取得最小值
.
| m |
| n |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
∴函数f(x)的单调递增区间为[-
| π |
| 12 |
| 5π |
| 12 |
(II)由f(
| A |
| 2 |
| π |
| 3 |
| π |
| 3 |
(i)∵acosB+bcosA=csinC,利用正弦定理可得sinAcosB+sinBcosA=sinCsinC,化为sin(A+B)=sinCsinC,即sinC=sinCsinC,∵0<C<π,∴sinC≠0.
∴sinC=1,∴C=
| π |
| 2 |
| π |
| 6 |
| AB |
| AC |
(
|
|
|
| AB |
| AC |
| π |
| 3 |
| AB |
| AC |
(1+λ+λ2)|
|
(λ+
|
| 1 |
| 2 |
3
| ||
| 2 |
点评:本题主要考查了平面向量、三角函数恒等变换、三角函数性质及其解三角形等基础知识,考查了计算能力和推理论证能力,考查了函数与方程思想、数形结合思想、转化与化归思想方法,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
在复平面内,复数z=
的虚部为( )
| 5i |
| 2i-1 |
| A、1 | B、-1 | C、i | D、-i |
已知函数f(x)=kx+1,其中实数k随机取自区间[-2,1],则对于?x∈[-1,1],都有f(x)≥0恒成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
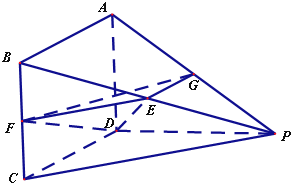 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.