题目内容
一个等差数列共有10项，其中奇数项的和为
，偶数项的和为15，则这个数列的第6项是（ ）
| 25 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用奇数项的和为
，偶数项的和为15，求出首项a1和公差d的值，可得数列的通项，从而可求数列的第6项．
| 25 |
| 2 |
解答：
解：设公差为d，则
∵奇数项的和为
，偶数项的和为15，
∴5a1+20d=
，5（a1+d）+20d=15，
解得a1=
，d=
，∴an=
+
（n-1）=
，n∈N+，
∴这个数列的第6项是3，
故选：A．
∵奇数项的和为
| 25 |
| 2 |
∴5a1+20d=
| 25 |
| 2 |
解得a1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∴这个数列的第6项是3，
故选：A．
点评：本题考查等差数列的定义，通项公式，前n项和公式的应用，求出首项a1和公差d的值，是解题的关键．
练习册系列答案
相关题目
已知函数f（x）sinωx+cosωx，如果存在实数x1，使得对任意的实数x，都有f（x1）≤f（x）≤f（x1+2014）成立，则ω的最小正值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设复数z=
，则z的共轭复数
为（ ）
| 1-i |
| 1+i |
. |
| z |
| A、1 | B、-1 | C、-i | D、i |
已知a=log23，b=ln2，c=5 -
，则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| A、a＞c＞b |
| B、a＞b＞c |
| C、b＞a＞c |
| D、b＞c＞a |
已知函数f（x）=kx+1，其中实数k随机取自区间[-2，1]，则对于?x∈[-1，1]，都有f（x）≥0恒成立的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin（α-
）=
，则cos（
+α）的值为（ ）
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
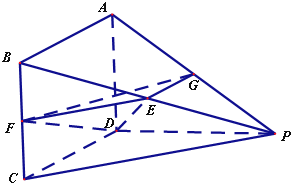如图，在四棱锥P-ABCD中，四边形ABCD是正方形，CD=PD，∠ADP=90°，∠CDP=120°，E，F，G分别为PB，BC，AP的中点．