题目内容
若复数z满足(1+i)z=i,则复数z的虚部为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:根据复数的有关概念,即可得到结论.
解答:
解:∵(1+i)z=i,
∴z=
=
=
=
+
i,
故复数z的虚部为
,
故选:A
∴z=
| i |
| 1+i |
| i(1-i) |
| (1+i)(1-i) |
| i+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故复数z的虚部为
| 1 |
| 2 |
故选:A
点评:本题主要考查复数的有关概念和运算,利用复数的四则运算是解决本题的关键,比较基础.

练习册系列答案
相关题目
已知x∈R,则“x≥1”是“
≤1”的( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知2弧度的圆心角所对的弦长为2,那么此圆心角所夹扇形的面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、tan1 |
已知函数f(x)=kx+1,其中实数k随机取自区间[-2,1],则对于?x∈[-1,1],都有f(x)≥0恒成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知对于正项数列{an}满足am+n=am•an(m,n∈N*),若a2=9,则log3a1+log3a2+…+log3a12=( )
| A、40 | B、66 | C、78 | D、156 |
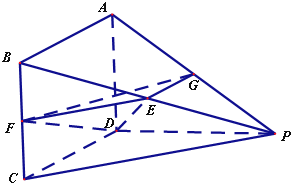 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.