Question

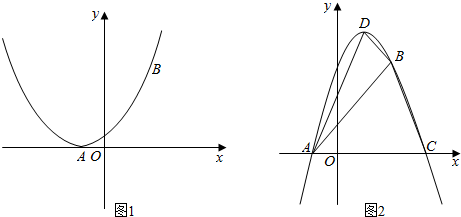
16．已知抛物线的表达式是y=ax²+（1-a）x+1-2a（a为常数且不为0），无论a为何值，上述抛物线始终经过x轴上的一定点A与第一象限内的另一定点B．
（1）如图1，当抛物线与x轴只有一个公共点时，求a的值；
（2）请写出A，B两点的坐标：A（-1，0），B（2，3）；
（3）如图2，当a＜0时，若上述抛物线顶点是D，与x轴的另一交点为点C，且点A，B，C，D中没有两个点相互重合．
①△ABC能否是直角三角形，为什么？
②若使得△ABD是直角三角形，请你求出a的值（求出1个a的值即可）．

Answer 1

分析 （1）由题意可得判别式为0，解方程可得a的值；
（2）由y=ax²+（1-a）x+1-2a可得，a（x²-x-2）+（1+x-y）=0，即为x²-x-2=0，1+x-y=0，解方程可得定点A，B的坐标；
（3）①若△ABC是直角三角形，即有B为直角顶点．设出C的坐标，由两直线垂直的条件：斜率之积为-1，计算即可得到结论；
②若使得△ABD是直角三角形，即有D为直角顶点，由二次函数的顶点坐标，结合两直线垂直的条件：斜率之积为-1，解方程可得a的值．

解答 解：（1）由题意可得判别式为0，即有△=（1-a）²-4a（1-2a）=0，
解得a=$\frac{1}{3}$；
（2）由y=ax²+（1-a）x+1-2a可得，
a（x²-x-2）+（1+x-y）=0，
即有$\left\{\begin{array}{l}{{x}^{2}-x-2=0}\\{x+1=y}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$；即A（-1，0），B（2，3）
故答案为：-1，2，3．
（3）①若△ABC是直角三角形，即有B为直角顶点．
设C（c，0），又A（-1，0），B（2，3），
由AB⊥BC，可得k_AB•k_BC=-1，
即为$\frac{3-0}{2+1}$•$\frac{3}{2-c}$=-1，解得c=5，
由f（5）=0，可得25a+5（1-a）+1-2a=0，
解得a=-$\frac{1}{3}$＜0，故存在△ABC是直角三角形；
②若使得△ABD是直角三角形，即有D为直角顶点，
由二次函数的顶点坐标可得D（$\frac{a-1}{2a}$，$\frac{6a-9{a}^{2}-1}{4a}$），
由AD⊥BD，可得k_AD•k_BD=-1，即有$\frac{\frac{6a-9{a}^{2}-1}{4a}}{\frac{a-1}{2a}+1}$•$\frac{\frac{6a-9{a}^{2}-1}{4a}-3}{\frac{a-1}{2a}-2}$=-1，化简可得81a4-54a2+5=0，
解得a=-$\frac{1}{3}$或-$\frac{\sqrt{5}}{3}$（正的舍去）．

点评 本题考查二次函数的图象和性质，同时考查两直线垂直的条件：斜率之积为-1，曲线恒过定点的求法，属于中档题．