题目内容
若y=a-bsinx的最大值为
,最小值为-
,求y=2asinx+b的最值.
| 3 |
| 2 |
| 1 |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:由条件求得a、b的值,可得函数y的解析式,再利用正弦函数的值域求得y=2asinx+b的最值.
解答:
解:由y=a-bsinx的最大值为
,最小值为-
,可得a+|b|=
,a-|b|=
,
求得a=1,|b|=
,∴a=1,且 b=±
.
故y=2asinx+b=2sinx+
,或 y=2sinx-
.
当y=2sinx+
时,最大值为2+
=
,最小值为-2+
=-
;
当y=2sinx-
时,最大值为2-
=
,最小值为-2-
=-
.
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
求得a=1,|b|=
| 1 |
| 2 |
| 1 |
| 2 |
故y=2asinx+b=2sinx+
| 1 |
| 2 |
| 1 |
| 2 |
当y=2sinx+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当y=2sinx-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查正弦函数的值域,求三角函数的最值,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
直角坐标系中,y=ax+
与y=ax2的图象可能是( )
| 1 |
| a |
A、 |
B、 |
C、 |
D、 |
 给出的是计算
给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
| A、I<=100 |
| B、I>100 |
| C、I>50 |
| D、I<=50 |
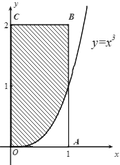 如图所示,在矩形OABC内任取一点P,则点P恰落在图中阴影部分中的概率为
如图所示,在矩形OABC内任取一点P,则点P恰落在图中阴影部分中的概率为