题目内容
设数列{an}满足an+1=
+
,(n∈N*).
(Ⅰ)若a1>
,证明:数列{an}单调递减;
(Ⅱ)若a1=2,证明:
<an<
+
.
| an |
| 2 |
| 1 |
| an |
(Ⅰ)若a1>
| 2 |
(Ⅱ)若a1=2,证明:
| 2 |
| 2 |
| 1 |
| n |
考点:数列递推式
专题:等差数列与等比数列
分析:(I)由a1>
,可得an>0,当n≥1时,利用基本不等式的性质可得an+1=
+
>
,(n∈N*).可得对一切n∈N*,都有an>
.再证明an+1-an<0即可.
(Ⅱ)由a1=2>
,由(Ⅰ)中可知an>
. 用数学归纳法证明an<
+
即可.
| 2 |
| an |
| 2 |
| 1 |
| an |
| 2 |
| 2 |
(Ⅱ)由a1=2>
| 2 |
| 2 |
| 2 |
| 1 |
| n |
解答:
证明:(Ⅰ)∵a1>
,∴an>0,
当n≥1时,an+1=
+
>2
=
.
∴对一切n∈N*,都有an>
.
∵an+1-an=
-
=
<0,
∴数列{an}单调递减.
(Ⅱ)∵a1=2>
,由(Ⅰ)中可知an>
.
下面用数学归纳法证明an<
+
①当n=1时,a1=2<
+
显然成立.
②假设n=k(k≥1)时,命题成立,即ak<
+
成立.
那么当n=k+1时,
有ak+1=
+
<
+
=
+
≤
+
∴当n=k+1时,上述命题也成立
综合①②可得对于任意n∈N*,有an<
+
.
因此,
<an<
+
.
| 2 |
当n≥1时,an+1=
| an |
| 2 |
| 1 |
| an |
|
| 2 |
∴对一切n∈N*,都有an>
| 2 |
∵an+1-an=
| 1 |
| an |
| an |
| 2 |
2-
| ||
| 2an |
∴数列{an}单调递减.
(Ⅱ)∵a1=2>
| 2 |
| 2 |
下面用数学归纳法证明an<
| 2 |
| 1 |
| n |
①当n=1时,a1=2<
| 2 |
| 1 |
| n |
②假设n=k(k≥1)时,命题成立,即ak<
| 2 |
| 1 |
| k |
那么当n=k+1时,
有ak+1=
| ak |
| 2 |
| 1 |
| ak |
| ||||
| 2 |
| 1 | ||
|
| 2 |
| 1 |
| 2k |
| 2 |
| 1 |
| k+1 |
∴当n=k+1时,上述命题也成立
综合①②可得对于任意n∈N*,有an<
| 2 |
| 1 |
| n |
因此,
| 2 |
| 2 |
| 1 |
| n |
点评:本题考查了数列的单调性、基本不等式的性质、数学归纳法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
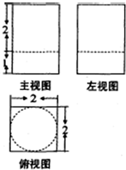 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A、12+π | B、6+π |
| C、12-π | D、6-π |
函数y=
的图象( )
| 4x-1 |
| 2x |
| A、关于直线y=-x对称 |
| B、关于原点对称 |
| C、关于y轴对称 |
| D、关于直线y=x对称 |