题目内容
3.椭圆满足这样的光学性质:从椭圆的一个焦点发射光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现在设有一个水平放置的椭圆形台球盘,满足方程:$\frac{x^2}{16}+\frac{y^2}{9}$=1,点A,B是它的两个焦点,当静止的小球放在点A处,从A点沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的最长路程是( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
分析 根据椭圆的光学性质可知,当静止的小球放在点A处,从点A沿直线出发,射到左顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a-c);射到右顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a+c);小球从点A沿直线出发,经椭圆壁反弹到B点继续前行碰椭圆壁后回到A点,所走的轨迹正好是两次椭圆上的点到两焦点距离之和4a,进而根据椭圆的定义可求得小球经过的最长路程.
解答 解:依题意可知$\frac{x^2}{16}+\frac{y^2}{9}$=1中,a=4,b=3,c=$\sqrt{7}$,设A,B分别为左、右焦点,
则当静止的小球放在点A处,从点A沿直线出发,射到左顶点,经椭圆壁反弹后,
再回到点A时,小球经过的路程是2(a-c)=2(2-$\sqrt{7}$);
射到右顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a+c)=2(2+$\sqrt{7}$);
小球经两次椭圆壁后反弹后回到A点,根据椭圆的性质可知所走的路程正好是4a=4×4=16,
小球经过的最长路程16,
故选C.
点评 本题主要考查了椭圆的应用.解题的关键是利用了椭圆的第一定义,属于基础题.

练习册系列答案
相关题目
14.设复数z=$\frac{2+i}{(1+i)^{2}}$(i为虚数单位),则z的虚部是( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
18.设条件p:x>0,条件q:x>1,则条件p是条件q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
8.已知定义在(0,+∞)的函数f(x)=|4x(1-x)|,若关于x的方程f2(x)+(t-3)f(x)+t-2=0有且只有3个不同的实数根,则实数t的取值集合是{2,$5-2\sqrt{2}$}.
13.在《九章算术》中有一个古典名题“两鼠穿墙”问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢?大意是有厚墙五尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半,问几天后两鼠相遇?( )
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
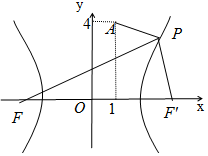 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求: