题目内容
15.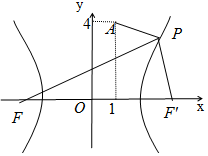 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:(1)|PF|+|PA|的最小值;
(2)|PF|-|PA|的有没有最大值?若有,求此最大值,并说明理由.
分析 (1)设双曲线的右焦点为F',求出双曲线的a,b,c,以及焦点坐标,运用双曲线的定义和三点共线,可得最小值为|AF'|;
(2)延长FA交双曲线右支于P,由|PF|-|PA|≤|AF|,结合渐近线的斜率和直线AF的斜率的关系,计算即可得到所求最大值.
解答 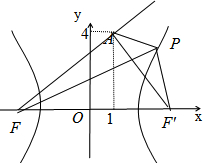 解:(1)设双曲线的右焦点为F',
解:(1)设双曲线的右焦点为F',
双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的a=2,b=2$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=4,
可得F(-4,0),F'(4,0),
由双曲线的定义可得|PF|-|PF'|=2a=4,
可得|PF|=4+|PF'|,
则|PF|+|PA|=4+|PF'|+|PA|≥|AF'|,当A,P,F'共线时,取得等号.
|AF'|=$\sqrt{(1-4)^{2}+(4-0)^{2}}$=5.
可得|PF|+|PA|的最小值为5;
(2)|PF|-|PA|≤|AF|,当A,P,F三点共线时,取得等号.
延长FA交双曲线右支于P,由双曲线的渐近线的斜率为±$\sqrt{3}$,
直线AF的斜率为$\frac{4-0}{1+4}$=$\frac{4}{5}$<$\sqrt{3}$,则P点存在.
|AF|=$\sqrt{(1+4)^{2}+(4-0)^{2}}$=$\sqrt{41}$.
则|PF|-|PA|的最大值为$\sqrt{41}$.
点评 本题考查双曲线的方程和性质,主要是定义法的运用,以及三点共线取得最值,考查数形结合思想方法,属于中档题.

练习册系列答案
相关题目
10.函数y=f(2x-1)是偶函数,则函数y=f(2x+1)的对称轴是( )
| A. | x=-1 | B. | x=0 | C. | $x=\frac{1}{2}$ | D. | $x=-\frac{1}{2}$ |
5.有两张卡片,一张的正反面分别画着老鼠和小鸡,另一张的正反面分别画着老鹰和蛇,现在有两个小孩随机地将两张卡片排在一起放在桌面上,不考虑顺序,则向上的图案是老鹰和小鸡的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
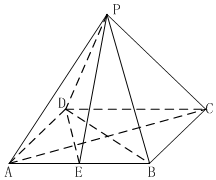 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.