题目内容
3.在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系,曲线C1的极坐标方程为$ρcos({θ-\frac{π}{3}})=1$,P为C1与x轴的交点,已知曲线C2的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=-2+sinθ\end{array}\right.$(θ为参数),M,N是曲线C2上的两点且对应的参数分别为θ=α,$θ=α+\frac{π}{2}$,其中α∈R.(Ⅰ)写出曲线C1的直角坐标方程;
(Ⅱ)求|PM|2+|PN|2的取值范围.
分析 (I)曲线C1的极坐标方程为$ρcos({θ-\frac{π}{3}})=1$,展开为:$ρ(\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ)$=1,利用互化公式可得直角坐标方程.
(II)由方程:x+$\sqrt{3}$y-2=0,可得∴P(2,0).M(cosα,-2+sinα),N(-sinα,-2+cosα).利用两点之间距离公式、同角三角函数基本关系式及其三角函数的单调性即可得出.
解答 解:(I)曲线C1的极坐标方程为$ρcos({θ-\frac{π}{3}})=1$,
展开为:$ρ(\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ)$=1,
化为直角坐标方程:x+$\sqrt{3}$y-2=0.
(II)由方程:x+$\sqrt{3}$y-2=0,令y=0,解得x=2.
∴P(2,0).M(cosα,-2+sinα),N(-sinα,-2+cosα).
∴|PM|2+|PN|2=(cosα-2)2+(sinα-2)2+(sinα+2)2+(cosα-2)2=18-8cosα∈[10,26].
点评 本题考查了极坐标方程化为直角坐标方程、两点之间距离公式、同角三角函数基本关系式及其三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若点M(x,y)为平面区域$\left\{\begin{array}{l}x+y≥2\\ x≤1\\ y≤2\end{array}\right.$上的一个动点,则x-y的取值范围是( )
| A. | [-2,0] | B. | [-1,0] | C. | [-1,-2] | D. | [0,2] |
11.已知全集U=R,A={x|x2-3x-4>0},B={x|-2≤x≤2},则如图所示的阴影部分所表示的集合为( )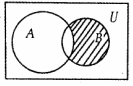

| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |
8.已知全集U={0,1,2,3,4},集合M={1,2,3},N={0,3,4},则(∁UM)∩N( )
| A. | {0,4} | B. | {3,4} | C. | {1,2} | D. | ∅ |
2.某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.