题目内容
9.已知函数f(x)=(x2-3)ex,设关于x的方程${f^2}(x)-mf(x)-\frac{12}{e^2}=0(m∈R)$有n个不同的实数解,则n的所有可能的值为( )| A. | 3 | B. | 1或3 | C. | 4或6 | D. | 3或4或6 |
分析 利用导数求出函数的单调性,画出图象,令f(x)=t,则方程${t^2}-mt-\frac{12}{e^2}=0$必有两根t1,t2(t1<t2)且${t_1}{t_2}=-\frac{12}{e^2}$,根据图象求解
解答 解:f′(x)=(x-1)(x+3)ex,∴f(x)在(-∞,-3)和(1,+∞)上单增,(-3,1)上单减,又当x→-∞时f(x)→0,x→+∞时f(x)→+∞,故f(x)的图象大致为: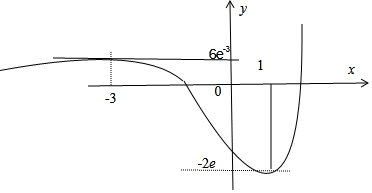
令f(x)=t,则方程${t^2}-mt-\frac{12}{e^2}=0$必有两根t1,t2(t1<t2)且${t_1}{t_2}=-\frac{12}{e^2}$,
当t1=-2e时恰有${t_2}=6{e^{-3}}$,此时f(x)=t1有1个根,f(x)=t2有2个根;
当t1<-2e时必有$0<{t_2}<6{e^{-3}}$,此时f(x)=t1无根,f(x)=t2有3个根;
当-2e<t1<0时必有${t_2}>6{e^{-3}}$,此时f(x)=t1有2个根,f(x)=t2有1个根;
综上,对任意m∈R,方程均有3个根.
故选:A.
点评 本题考查了方程的根与函数图象交点间的转化,方程与函数的思想、数形结合的思想是解题的关键,属于难题.

练习册系列答案
相关题目
17.取一个长度为4m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不少于1m的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
4.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(1,\sqrt{3})$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a|$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
14.“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
3.已知命题:?x∈R,x2-ax+2a>0在R上恒成立,则实数a的取值范围是( )
| A. | (0,4) | B. | (-8,8) | C. | R | D. | (0,8) |
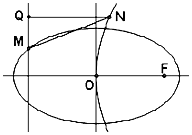 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.