题目内容
下列说法正确的是( )
A、函数f(x)=
| ||
| B、两个三角形全等是这两个三角形面积相等的必要条件 | ||
| C、命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013<0” | ||
| D、给定命题p、q,若p∧q是真命题,则¬p是假命题 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据反比例函数的单调性,必要条件,充分条件的概念,命题的否命题,p∧q,¬p的真假和p,q真假的关系即可找出说法正确的选项.
解答:
解:A.不正确,f(x)=
的定义域不连续,所以在定义域上不具有单调性;
B.不正确,若两个三角形全等,则这两个三角形面积相等,所以是充分条件;
C.不正确,命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013≤0”;
D.正确,若p∧q为真命题,则p是真命题,∴¬p是假命题.
故选D.
| 1 |
| x |
B.不正确,若两个三角形全等,则这两个三角形面积相等,所以是充分条件;
C.不正确,命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013≤0”;
D.正确,若p∧q为真命题,则p是真命题,∴¬p是假命题.
故选D.
点评:考查反比例函数的单调性,充分条件,必要条件的概念,命题的否定,以及p∧q,¬p的真假和p,q真假的关系.

练习册系列答案
相关题目
若a、b、c为实数,则下列命题正确的是( )
| A、若a>b,则ac2>bc2 | ||||
| B、若a<b<0,则a2>ab>b2 | ||||
C、若a<b,则
| ||||
D、若a>b>0,则
|
“α>β”是“sinα>sinβ”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
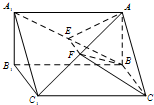 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.