题目内容
20.设向量$\overrightarrow{a}$=(4,m),$\overrightarrow{b}$=(1,-2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{10}$.分析 $\overrightarrow{a}$⊥$\overrightarrow{b}$,可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,解得m.再利用模的计算公式即可得出.
解答 解:∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$=4-2m=0,
解得m=2.
∴$\overrightarrow{a}$-2$\overrightarrow{b}$=(2,6).
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$.
故答案为:$2\sqrt{10}$.
点评 本题考查了向量垂直与数量积的关系、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.若复数z=$\frac{1-3i}{1+i}$(i为虚数单位),则|z+1|=( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
5.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(m+1,-m),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m的值为( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
10.若点P(sinθ,cosθ)在直线2x+y=0上,则tan2θ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | -$\frac{4}{3}$ | D. | $\frac{4}{5}$ |
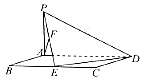 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点. 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4$\sqrt{5}$.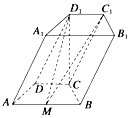 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.