题目内容
数列{an}各项均为正数,Sn为其前n项和,a1=-1,对于n∈N+.总有an2,2Sn,an+12成等比数列.
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和Tn=2an-b,求证:bn=2-
.
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和Tn=2an-b,求证:bn=2-
| 1 |
| 2n-1 |
考点:数列递推式,数列的应用
专题:等差数列与等比数列
分析:(1)根据an2,2S,an+12成等比数列结合an>0得到2Sn=anan+1,由此得到an+1-an-1=2.说明数列的奇数项和偶数项均构成等差数列,得到数列{an}是首项为1公差为1的等差数列.则数列的通项公式可求;
(2)把{an}的通项公式代入Tn=2an-bn,整理后构造等比数列{bn-2},求出其通项公式后得答案.
(2)把{an}的通项公式代入Tn=2an-bn,整理后构造等比数列{bn-2},求出其通项公式后得答案.
解答:
解:(1)由an2,2Sn,an+12成等比数列,得4Sn2=an2an+12.
又an>0,∴2Sn=anan+1,则2a1=a1a2,
又a1=1,∴a2=2.
当n>1时,2Sn-1=an-1an.
∴2an=an(an+1-an-1),即an+1-an-1=2.
∵a1=1,a2=2,
∴a1,a3,a5,…成首项为1,公差为2的等差数列.
a2,a4,a6,…成首项为2公差为2的等差数列.
∴数列{an}是首项为1公差为1的等差数列.
∴an=n;
(2)∵Tn=2an-bn=2n-bn,
∴b1=2-b1,b1=1.
n>1时,Tn-1=2(n-1)-bn-1,
∴bn=2-bn+bn-1,
2bn=2+bn-1,
∴2(bn-2)=bn-1-2.
∴{bn-2}是首项为1-2=-1,公比为
的等比数列.
∴bn-2=-(
)n-1.
则bn=2-
.
又an>0,∴2Sn=anan+1,则2a1=a1a2,
又a1=1,∴a2=2.
当n>1时,2Sn-1=an-1an.
∴2an=an(an+1-an-1),即an+1-an-1=2.
∵a1=1,a2=2,
∴a1,a3,a5,…成首项为1,公差为2的等差数列.
a2,a4,a6,…成首项为2公差为2的等差数列.
∴数列{an}是首项为1公差为1的等差数列.
∴an=n;
(2)∵Tn=2an-bn=2n-bn,
∴b1=2-b1,b1=1.
n>1时,Tn-1=2(n-1)-bn-1,
∴bn=2-bn+bn-1,
2bn=2+bn-1,
∴2(bn-2)=bn-1-2.
∴{bn-2}是首项为1-2=-1,公比为
| 1 |
| 2 |
∴bn-2=-(
| 1 |
| 2 |
则bn=2-
| 1 |
| 2n-1 |
点评:本题考查了数列递推式,考查了等差关系和等比关系的确定,训练了数列构造法,是中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
复数Z=
,则复数
对应的点在( )
| ||
1-
|
. |
| Z |
| A、第一象限或第三象限 |
| B、y轴负半轴上 |
| C、x轴正半轴上 |
| D、第二象限或第四象限 |
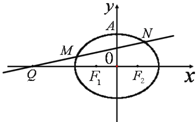 如图,已知椭圆C:
如图,已知椭圆C: