题目内容
已知集合A={x|ax-1>0},B={x|x2-3x+2>0}.
(1)若A∩B=A,求实数a的取值范围;
(2)若A∩∁RB≠∅,求实数a的取值范围.
(1)若A∩B=A,求实数a的取值范围;
(2)若A∩∁RB≠∅,求实数a的取值范围.
考点:补集及其运算,交集及其运算
专题:集合
分析:(1)若A∩B=A,则A⊆B,对a进行分类讨论后,综合讨论结果可得,实数a的取值范围;
(2)若A∩∁RB≠∅,则A≠∅,此时不等式ax-1>0解集的端点
∈∁RB时,满足条件,进而可求实数a的取值范围.
(2)若A∩∁RB≠∅,则A≠∅,此时不等式ax-1>0解集的端点
| 1 |
| a |
解答:
解:(1)∵B={x|x2-3x+2>0}={x|x<1,或x>2}
若A∩B=A,则A⊆B,
①当a=0时,A=∅,满足要求;
②当a>0时,A={x|x>
},则
≥2,解得0<a≤
,
③当a<0时,A={x|x<
},则
≤1,此时a<0,
综上所述实数a的取值范围为a≤
,
(2)由(1)得∁RB={x|1≤x≤2}
若A∩∁RB≠∅,则A≠∅,即a≠0,且
∈∁RB,
即1≤
≤2,
解得
≤a≤1
若A∩B=A,则A⊆B,
①当a=0时,A=∅,满足要求;
②当a>0时,A={x|x>
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
③当a<0时,A={x|x<
| 1 |
| a |
| 1 |
| a |
综上所述实数a的取值范围为a≤
| 1 |
| 2 |
(2)由(1)得∁RB={x|1≤x≤2}
若A∩∁RB≠∅,则A≠∅,即a≠0,且
| 1 |
| a |
即1≤
| 1 |
| a |
解得
| 1 |
| 2 |
点评:本题考查的知识点是交集,补集及其运算,难度不大,属于基础题.

练习册系列答案
相关题目
已知集合M={x|x≥-1},N={x|2-x2≥0},则M∪N=( )
A、[-
| ||
B、[-1,
| ||
| C、[-1,+∞) | ||
D、(-∞,-
|
 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.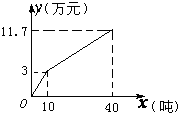 春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:
春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题: 如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,求它落在扇形外正方形内的概率.
如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,求它落在扇形外正方形内的概率.