题目内容
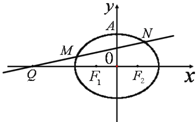 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)过点Q(-4,0)任作一动直线l交椭圆C于M,N两点,记
| MQ |
| QN |
| MR |
| RN |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得c=1,a=2,由此能求出椭圆C的方程.
(2)由题意知直线MN的斜率必存在,设其直线方程为y=k(x+4),设M(x1,y1),N(x2,y2),联立方程组
,得(3+4k2)x2+32k2x+64k2-12=0,由此利用向量知识、韦达定理,结合已知条件能求出点R在定直线x=-1上.
(2)由题意知直线MN的斜率必存在,设其直线方程为y=k(x+4),设M(x1,y1),N(x2,y2),联立方程组
|
解答:
(本小题满分10分)
解:(1)∵椭圆C:
+
=1,(a>b>0)的左、右焦点为F1、F2,其上顶点为A,
△F1AF2是边长为2的正三角形,
∴c=1,a=2,…(1分)
故椭圆C的方程为
+
=1.…(3分)
(2)由题意知直线MN的余率必存在,设其直线方程为y=k(x+4),
设M(x1,y1),N(x2,y2),联立方程组
,
消去y,得(3+4k2)x2+32k2x+64k2-12=0,
∴△=144(1-4k2)>0,x1+x2=
,x1x2=
,
由
=λ•
,得-4-x1=λ(x2+4),
解得λ=-
,
设点R的坐标为(x0,y0),则由
=-λ•
,
得x0-x1=-λ(x2-x0),
解得x0=
=
=
,
又2x1x2+4(x1+x2)=2×
+4×
=
,
(x1+x2)+8=
+8=
,
从而x0=
=-1,
故点R在定直线x=-1上.
解:(1)∵椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
△F1AF2是边长为2的正三角形,
∴c=1,a=2,…(1分)
故椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意知直线MN的余率必存在,设其直线方程为y=k(x+4),
设M(x1,y1),N(x2,y2),联立方程组
|
消去y,得(3+4k2)x2+32k2x+64k2-12=0,
∴△=144(1-4k2)>0,x1+x2=
| -32k2 |
| 3+4k2 |
| 64k2-12 |
| 3+4k2 |
由
| MQ |
| QN |
解得λ=-
| x1+4 |
| x2+4 |
设点R的坐标为(x0,y0),则由
| MR |
| RN |
得x0-x1=-λ(x2-x0),
解得x0=
| x1-λx2 |
| 1-λ |
x1+
| ||
1+
|
| 2x1x2+4(x1+x2) |
| (x1+x2)+8 |
又2x1x2+4(x1+x2)=2×
| 64k2-12 |
| 3+4k2 |
| -32k2 |
| 3+4k2 |
| -24 |
| 3+4k2 |
(x1+x2)+8=
| -32k2 |
| 3+4k2 |
| 24 |
| 3+4k2 |
从而x0=
| 2x1x2+4(x1+x2) |
| (x1+x2)+8 |
故点R在定直线x=-1上.
点评:本题考查椭圆方程的求法,考查点是否在在定直线上的判断与求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
sin2013°的值属于区间( )
A、(-
| ||
B、(-1,-
| ||
C、(
| ||
D、(0,
|
 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.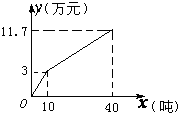 春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:
春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题: