题目内容
14.将棱长为2的正四面体木块切削成一个体积最大的球,则该球的体积是( )| A. | $\frac{\sqrt{6}π}{27}$ | B. | $\sqrt{6}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{4}{3}$π |
分析 由题意,所求球为正四面体ABCD的内切球,如图O为正四面体ABCD的内切球的球心,说明OE是内切球的半径,运用勾股定理计算,即可得到球的体积.
解答  解:由题意,所求球为正四面体ABCD的内切球,如图O为正四面体ABCD的内切球的球心,
解:由题意,所求球为正四面体ABCD的内切球,如图O为正四面体ABCD的内切球的球心,
正四面体的棱长为2,
所以OE为内切球的半径,设OA=OB=R,
在等边三角形BCD中,BE=$\frac{\sqrt{3}}{3}$×2=$\frac{2\sqrt{3}}{3}$,
AE=$\sqrt{4-\frac{4}{3}}$=$\frac{2\sqrt{6}}{3}$.
由OB2=OE2+BE2,即有R2=($\frac{2\sqrt{6}}{3}$-R)2+$\frac{4}{3}$
解得,R=$\frac{\sqrt{6}}{2}$.OE=AE-R=$\frac{\sqrt{6}}{6}$,
则其内切球的半径是$\frac{\sqrt{6}}{6}$,
内切球的体积为$\frac{4}{3}π$×($\frac{\sqrt{6}}{6}$)3=$\frac{\sqrt{6}}{27}π$.
故选:A.
点评 本题考查正四面体的内切球半径的求法,内切球的半径是正四面体的高的$\frac{1}{4}$,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
9.已知公比为q的等比数列{an},且满足条件|q|>1,a2+a7=2,a4a5=-15,则a12=( )
| A. | -$\frac{27}{25}$ | B. | -$\frac{25}{3}$ | C. | -$\frac{27}{25}$或-$\frac{25}{3}$ | D. | $\frac{25}{3}$ |
19.已知α是第二象限角,则由sinα=$\frac{\sqrt{3}}{2}$可推出cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
6.已知向量$\overrightarrow{a}$=(1,2),则|$\overrightarrow{a}$|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
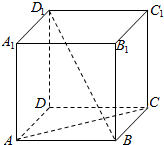 已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.
已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.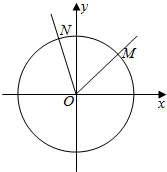 如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.
如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.