题目内容
5.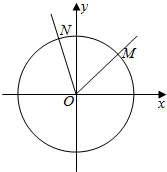 如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.
如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.(I)求函数f(α)的值域;
(Ⅱ)在△ABC中,角A,B,C所对的边是a,b,c.若f(C)=$\sqrt{3}$,c=7,sinA+sinB=$\frac{13\sqrt{3}}{14}$,求△ABC的面积.
分析 (I)根据三角函数的定义求出函数f(α)的表达式,即可求出处函数的值域;
(Ⅱ)由f(C)=$\sqrt{3}$,可得:sin(C+$\frac{π}{6}$)=1,结合范围0<C<π,解得C=$\frac{π}{3}$,由条件c=7,sinA+sinB=$\frac{13\sqrt{3}}{14}$,结合正弦定理可得a+b=13,由余弦定理可得ab=40,利用三角形面积公式即可得解.
解答 解:(Ⅰ)∵由三角函数定义知,y1=sinα,y2=sin(α+$\frac{π}{3}$),
∴f(α)=y1+y2=sinα+sin(α+$\frac{π}{3}$)=$\sqrt{3}$sin(α+$\frac{π}{6}$),
∵角α为锐角,
∴$\frac{π}{6}$<α+$\frac{π}{6}$<$\frac{2π}{3}$,
∴$\frac{1}{2}$<sin(α+$\frac{π}{6}$)≤1,
∴$\frac{\sqrt{3}}{2}$<$\sqrt{3}$sin(α+$\frac{π}{6}$)≤$\sqrt{3}$,
则f(α)的取值范围是($\frac{\sqrt{3}}{2}$,$\sqrt{3}$];
(Ⅱ)∵f(C)=$\sqrt{3}$sin(C+$\frac{π}{6}$)=$\sqrt{3}$,可得:sin(C+$\frac{π}{6}$)=1,
∵0<C<π,$\frac{π}{6}$<C+$\frac{π}{6}$<$\frac{7π}{6}$,解得:C+$\frac{π}{6}$=$\frac{π}{2}$,即C=$\frac{π}{3}$.
∵c=7,sinA+sinB=$\frac{13\sqrt{3}}{14}$,
∴由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{7}{\frac{\sqrt{3}}{2}}$,可得:a+b=13,
∴由余弦定理可得:49=a2+b2-ab=(a+b)2-3ab=169-3ab,解得:ab=40,
∴${S}_{△ABC}=\frac{1}{2}$absinC=$\frac{1}{2}×40×\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
点评 本题主要考查三角函数的定义以及正弦定理,余弦定理,三角形面积公式的应用,考查了正弦函数的图象和性质,考查了计算能力和转化思想,属于中档题.

| A. | $\frac{2014}{2015}$ | B. | $\frac{{2}^{2015}-1}{{2}^{2015}}$ | C. | $\frac{{2}^{2014}-1}{{2}^{2014}}$ | D. | $\frac{{2}^{2016}-1}{{2}^{2016}}$ |
| A. | $\frac{\sqrt{6}π}{27}$ | B. | $\sqrt{6}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{4}{3}$π |
| A. | f(4)>f(-6) | B. | f(-4)<f(-6) | C. | f(-4)>f(-6) | D. | f(4)<f(-6) |