题目内容
已知在△A BC中,角 A,B,C所对的边分别为a,b,c.已知c=2,sinC(
sinB+cosB)=sinA.
(Ⅰ)求角C的大小;
(Ⅱ)若cosA=
,求边b的长.
| 3 |
(Ⅰ)求角C的大小;
(Ⅱ)若cosA=
2
| ||
| 3 |
考点:正弦定理
专题:计算题,解三角形
分析:(Ⅰ)由已知可得
sinBsinC=sinBcosC,即tanC=
,从而可求C的值.
(Ⅱ)先求得sinA的值,由sinB=sin(A+C)=sinAcosC+sinCcosA,可求得sinB,根据正弦定理
=
,即可求得b的值.
| 3 |
| ||
| 3 |
(Ⅱ)先求得sinA的值,由sinB=sin(A+C)=sinAcosC+sinCcosA,可求得sinB,根据正弦定理
| c |
| sinC |
| b |
| sinB |
解答:
解:(本小题满分15分)
(Ⅰ)由已知可得
sinCsinB+sinCcosB=sinBcosC+sinCcosB…2分
即有
sinBsinC=sinBcosC,即tanC=
…5分
所以C=
…7分
(Ⅱ)因为sinA=
=
…9分
又因为sinB=sin(A+C)=sinAcosC+sinCcosA,
所以sinB=
…11分
根据正弦定理
=
,得b=
…14分
所以边b的长为:
…15分
(Ⅰ)由已知可得
| 3 |
即有
| 3 |
| ||
| 3 |
所以C=
| π |
| 6 |
(Ⅱ)因为sinA=
| 1-cos2A |
| 1 |
| 3 |
又因为sinB=sin(A+C)=sinAcosC+sinCcosA,
所以sinB=
| ||||
| 6 |
根据正弦定理
| c |
| sinC |
| b |
| sinB |
2
| ||||
| 3 |
所以边b的长为:
2
| ||||
| 3 |
点评:本题主要考查了正弦定理在解三角形中的应用,考查了两角和与差的正弦公式的应用,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
甲、乙、丙三位同学站成一排照相留念,则甲、乙相邻的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知四边形ABCD为梯形,AB∥CD,l为空间一直线,则“l垂直于两腰AD,BC”是“l垂直于两底AB,DC”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分不要条件 |
| D、既不充分也不必要条件 |

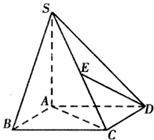 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,