题目内容
9.已知等差数列{an}的前n项和Sn=n2,则数列{an}的公差d=2.分析 由等差数列的前n项和求得等差数列的前2项,由d=a2-a1求得公差.
解答 解:∵等差数列{an}的前n项和Sn=n2,
∴a1=S1=1,a2=S2-S1=4-1=3,
∴公差d=a2-a1=3-1=2.
故答案为:2.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.直线l过点(1,0),且倾斜角为$\frac{5π}{6}$,则直线l的方程为( )
| A. | y=-$\frac{{\sqrt{3}}}{3}$x+1 | B. | y=$\frac{{\sqrt{3}}}{3}({x-1})$ | C. | y=-$\frac{{\sqrt{3}}}{3}$x-1 | D. | y=-$\frac{{\sqrt{3}}}{3}({x-1})$ |
4.复数$\frac{2-i}{1-i}$=( )
| A. | $\frac{3}{2}-\frac{i}{2}$ | B. | $\frac{3}{2}+\frac{i}{2}$ | C. | $-\frac{3}{2}+\frac{i}{2}$ | D. | $-\frac{3}{2}-\frac{i}{2}$ |
14.在Rt△ABC中,∠A=90°,AB=2,AC=4,E,F分别为AB,BC的中点,则$\overrightarrow{CE}•\overrightarrow{AF}$=( )
| A. | 9 | B. | -9 | C. | 7 | D. | -7 |
1.已知集合A={x|y=$\sqrt{x-3}$},B=(0,+∞),则A∩B=( )
| A. | (0,+∞) | B. | (3,+∞) | C. | [0,+∞) | D. | [3,+∞) |
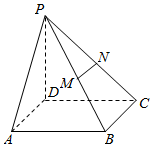 如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.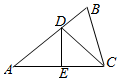 如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.
如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.