题目内容
13.已知x,y为正实数,则$\frac{4x}{x+3y}+\frac{3y}{x}$的最小值为( )| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 关键基本不等式的性质求出代数式的最小值即可.
解答 解:∵x,y为正实数,
∴$\frac{4x}{x+3y}+\frac{3y}{x}$
=$\frac{4}{1+\frac{3y}{x}}$+(1+$\frac{3y}{x}$)-1
≥2$\sqrt{\frac{4}{1+\frac{3y}{x}}(1+\frac{3y}{x})}$-1=4-1=3,
当且仅当${(1+\frac{3y}{x})}^{2}=4$即x=3y时“=”成立,
故选:D.
点评 本题考查了基本不等式的性质,注意应用性质的条件,本题是一道基础题.

练习册系列答案
相关题目
18.式子a2$\sqrt{a{b}^{3}\sqrt{a{b}^{5}}}$化简正确的是( )
| A. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{4}}$ | B. | a${\;}^{\frac{11}{4}}$b${\;}^{\frac{11}{2}}$ | C. | a${\;}^{\frac{11}{4}}$ | D. | b${\;}^{\frac{11}{4}}$ |
5.设a=ln2,b=log23,c=log3$\frac{1}{2}$,则a,b,c的大小关系是( )
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | c>b>a |
 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km,试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式.
一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.假设这辆汽车的里程表在汽车行驶这段路程前的读数为2000km,试建立行驶这段路程时汽车里程表读数s 与时间t 的函数解析式.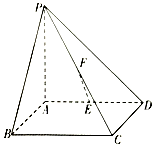 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.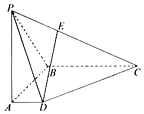 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.