题目内容
已知向量
=(1,2),
=(0,-1),
=(k,-2),若(
-2
)⊥
,则实数k= .
| a |
| b |
| c |
| a |
| b |
| c |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由题意可得
-2
的坐标,由(
-2
)⊥
,可得(
-2
)•
=0,代入数据解关于k的方程可得.
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
解答:
解:由题意可得
-2
=(1,2)-2(0,-1)=(1,4),
∵(
-2
)⊥
,∴(
-2
)•
=0,
代入数据可得1×k+4×(-2)=0,
解得k=8
故答案为:8
| a |
| b |
∵(
| a |
| b |
| c |
| a |
| b |
| c |
代入数据可得1×k+4×(-2)=0,
解得k=8
故答案为:8
点评:本题考查向量的垂直与数量积的关系,属基础题.

练习册系列答案
相关题目
已知曲线y=
x3+
x2+4x-7在点Q处的切线的倾斜角α满足sin2α=
,则此切线的方程为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 17 |
A、4x-y+7=0或4x-y-6
| ||
B、4x-y-6
| ||
C、4x-y-7=0或4x-y-6
| ||
| D、4x-y-7=0 |
已知点A(1,-2),若向量
与
=(2,3)同向,且|
|=2
,则点B的坐标为( )
. |
| AB |
| a |
| AB |
| 13 |
| A、(5,-4) |
| B、(4,5) |
| C、(-5,-4) |
| D、(5,4) |
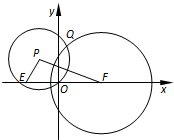 如图,已知O(0,0),E(-
如图,已知O(0,0),E(- 如图,正三棱柱ABC-A1B1C1的底面边长为a,当正视图的视线方向垂直于平面AA1B1B时,正视图的面积为2a2,则此时左视图的面积为
如图,正三棱柱ABC-A1B1C1的底面边长为a,当正视图的视线方向垂直于平面AA1B1B时,正视图的面积为2a2,则此时左视图的面积为