题目内容
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为________.
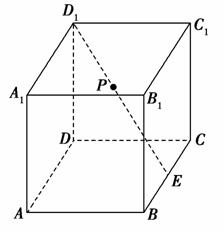
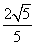
[解析] 过E点作EE1垂直底面A1B1C1D1,交B1C1于点E1,
连接D1E1,过P点作PH垂直于底面A1B1C1D1,交D1E1于点H,
P点到直线CC1的距离就是C1H,

故当C1H垂直于D1E1时,P点到直线CC1距离最小,
此时,在Rt△D1C1E1中,C1H⊥D1E1,D1E1·C1H=C1D1·C1E1,∴C1H= =
=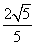 .
.

练习册系列答案
相关题目
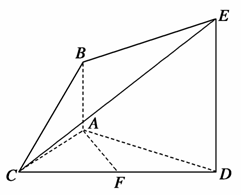
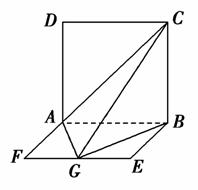
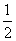 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )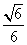 B.
B.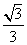
 D.
D.

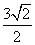
 D.
D.
 =
=