题目内容
已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心O在AB上,PO⊥平面ABC, =
= ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.
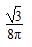 [解析]
[解析]
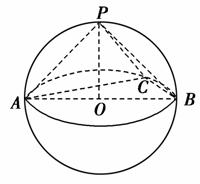
如图,依题意,AB=2R,又 =
= ,∠ACB=90°,因此AC=
,∠ACB=90°,因此AC= R,BC=R,VP-ABC=
R,BC=R,VP-ABC=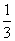 PO·S△ABC=
PO·S△ABC=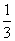 ×R×(
×R×( ×
× R×R)=
R×R)=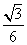 R3.而V球=
R3.而V球=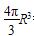 3,因此VP-ABCV球=
3,因此VP-ABCV球=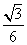 R3
R3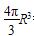 =
= 8π.
8π.

练习册系列答案
相关题目
题目内容
已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心O在AB上,PO⊥平面ABC, =
= ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.
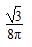 [解析]
[解析]

如图,依题意,AB=2R,又 =
= ,∠ACB=90°,因此AC=
,∠ACB=90°,因此AC= R,BC=R,VP-ABC=
R,BC=R,VP-ABC=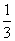 PO·S△ABC=
PO·S△ABC=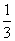 ×R×(
×R×( ×
× R×R)=
R×R)=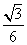 R3.而V球=
R3.而V球=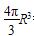 3,因此VP-ABCV球=
3,因此VP-ABCV球=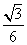 R3
R3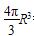 =
= 8π.
8π.
