题目内容
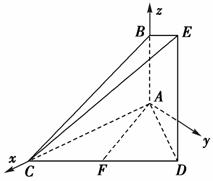
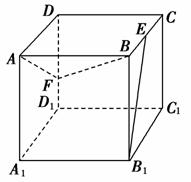
.如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
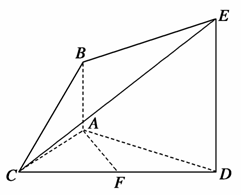
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
证法一:(1)
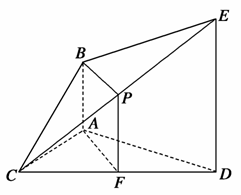
取CE的中点P,连接FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP= DE.
DE.
又AB∥DE,且AB= DE,
DE,
∴AB∥FP,且AB=FP,
∴四边形ABPF为平行四边形,∴AF∥BP.
又∵AF⊄平面BCE,BP⊂平面BCE,
∴AF∥平面BCE.
(2)∵△ACD为正三角形,∴AF⊥CD.
∵AB⊥平面ACD,DE∥AB,∴DE⊥平面ACD,
又AF⊂平面ACD,∴DE⊥AF.
又AF⊥CD,CD∩DE=D,∴AF⊥平面CDE.
又BP∥AF,∴BP⊥平面CDE.
又∵BP⊂平面BCE,∴平面BCE⊥平面CDE.
证法二:设AD=DE=2AB=2a,建立如图所示的坐标系A-xyz,则A(0,0,0),C(2a,0,0),B(0,0,a),D(a,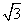 a,0),E(a,
a,0),E(a,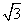 a,2a).
a,2a).
∵F为CD的中点,∴F(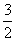 a,
a,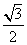 a,0).
a,0).
 又AF∥平面BCE,∴平面BCE⊥平面CDE.
又AF∥平面BCE,∴平面BCE⊥平面CDE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

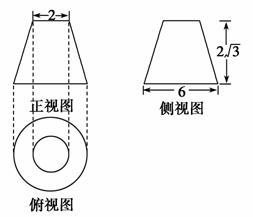
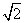 的等边三角形,AB=2,O是AB的中点.
的等边三角形,AB=2,O是AB的中点.
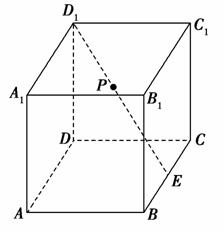
 的正三棱柱的各顶点均在同一个球面上,则该球的表面积为( )
的正三棱柱的各顶点均在同一个球面上,则该球的表面积为( )