题目内容
在△ABC中，∠C=90°，CD是斜边AB上的高．已知CD=
，BC=
，则AD=（ ）
| 2 |
| 6 |
| A、1 | B、2 | C、3 | D、4 |
考点：相似三角形的性质
专题：计算题,立体几何
分析：由Rt△ABC中，∠ACB=90°，CD是斜边上的高，根据有两角对应相等的三角形相似，易证得△ADC∽△CDB，然后由相似三角形的对应边成比例，即可求得答案．
解答：
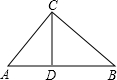解：∵Rt△ABC中，∠ACB=90°，CD是斜边上的高，
∴∠BDC=∠CBA，∠A=∠CDB，
∴△ADC∽△CDB，
∴
=
，
∵CD=
，BC=
，
∴DB=2，AD=1，
故选：A．
解：∵Rt△ABC中，∠ACB=90°，CD是斜边上的高，∴∠BDC=∠CBA，∠A=∠CDB，
∴△ADC∽△CDB，
∴
| AD |
| CD |
| DC |
| DB |
∵CD=
| 2 |
| 6 |
∴DB=2，AD=1，
故选：A．
点评：本题考查了直角三角形的性质和相似三角形的判定及性质的运用，在解答时运用直角三角形的性质求出角相等证明三角形相似是关健．
练习册系列答案
相关题目
袋中有20个大小相同的球，其中记上0号的有10个，记上n号的有n个（n=1，2，3，4）．现从袋中任取一球，ξ表示所取球的标号．若η=aξ-2，E（η）=1，则a的值为（ ）
| A、2 | B、-2 | C、1.5 | D、3 |
在等比数列{an}中，对任意正整数n有4an-4an+1+an+2=0，前99项的和S99=56，则a3+a6+a9+…+a99的值为（ ）
| A、16 | B、32 | C、64 | D、128 |
设函数f（x）=
sin（ωx+φ+
）（0＜φ＜
）的最小正周期为π，且f（-x）=f（x），则（ ）
| 2 |
| π |
| 4 |
| π |
| 2 |
A、f（x）在（0，
| ||||
B、f（x）在（
| ||||
C、f（x）在（0，
| ||||
D、f（x）在（
|
已知向量
=（1，k），
=（2，k-3），且
∥
，则k的值为（ ）
| a |
| b |
| a |
| b |
| A、-3 | B、0 | C、1 | D、3 |
下列函数f（x）中，在（0，+∞）上是减函数的是（ ）
A、f（x）=
| ||
| B、f（x）=x3 | ||
| C、f（x）=lnx | ||
| D、f（x）=2x |
圆的极坐标方程分别是ρ=2cosθ和ρ=4sinθ，两个圆的圆心距离是（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、5 |
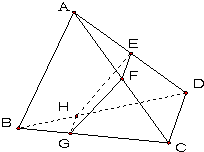如图，三棱锥A-BCD被一平面所截，截面为平行四边形EFGH，