题目内容
在平面直角坐标系中,已知动点M(x,y),点A(0,1)、B(0,-1),D(1,0),点N与点M关于直线y=x对称,且
•
=
x2,直线l是过点D的任意一条直线.
(1)求动点M所在曲线C的轨迹方程;
(2)设直线l与曲线C交于G、H两点,且|GH|=
,求直线l的方程;
(3)若直线l与曲线C交于G、H两点,与线段AB交于点P(点P不同于点O、A、B),直线GB与直线HA交于点O,求证:
•
是定值.
| AN |
| BN |
| 1 |
| 2 |
(1)求动点M所在曲线C的轨迹方程;
(2)设直线l与曲线C交于G、H两点,且|GH|=
3
| ||
| 2 |
(3)若直线l与曲线C交于G、H两点,与线段AB交于点P(点P不同于点O、A、B),直线GB与直线HA交于点O,求证:
| OP |
| OQ |
考点:直线与圆锥曲线的综合问题
专题:计算题,证明题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出N的坐标,运用向量的数量积的坐标表示,化简即可得到轨迹方程;
(2)设l:y=k(x-1),联立椭圆方程,消去y,运用韦达定理和弦长公式,即可求得斜率,进而得到直线方程;
(3)求出HA,GB的方程,设出Q的坐标,由(2)得,P(0,-k),再由直线GB与直线HA交于点O,解得Q的纵坐标,再由向量的数量积的坐标表示,即可得到定值1.
(2)设l:y=k(x-1),联立椭圆方程,消去y,运用韦达定理和弦长公式,即可求得斜率,进而得到直线方程;
(3)求出HA,GB的方程,设出Q的坐标,由(2)得,P(0,-k),再由直线GB与直线HA交于点O,解得Q的纵坐标,再由向量的数量积的坐标表示,即可得到定值1.
解答:
解:(1)由题意可得,N(y,x),
=(y,x-1),
=(y,x+1),
•
=
x2,
即有y2+x2-1=
x2,即有C:
+y2=1;
(2)若l平行于y轴,则|GH|=
,这与已知矛盾,则l不平行于y轴.
设l:y=k(x-1),联立椭圆方程,得(1+2k2)x2-4k2x+2k2-2=0,
设H(x1,y1),G(x2,y2),则x1+x2=
,x1x2=
,
且判别式大于0,又|GH|=
,
即
•
=
•
=
,解得,k=±
.
则l:y=±
(x-1);
(3)证明:由l与 AB交于P,且与点O,A,B不重合,
则l的斜率k:-1<k<1且k≠0,由(2)得,P(0,-k),
y1+y2=
,y1y2=
,
HA:y-1=
x,GB:y+1=
x.
Q(xQ,yQ),则有
=
•
则
>0,(
)2=
•
=
=(
)2,
则有
=
,解得,yQ=-
,
则有
•
=(0,-k)•(xQ,-
)=0+(-k)•(-
)=1为定值.
| AN |
| BN |
| AN |
| BN |
| 1 |
| 2 |
即有y2+x2-1=
| 1 |
| 2 |
| x2 |
| 2 |
(2)若l平行于y轴,则|GH|=
| 2 |
设l:y=k(x-1),联立椭圆方程,得(1+2k2)x2-4k2x+2k2-2=0,
设H(x1,y1),G(x2,y2),则x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
且判别式大于0,又|GH|=
3
| ||
| 2 |
即
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
|
=
3
| ||
| 2 |
| ||
| 2 |
则l:y=±
| ||
| 2 |
(3)证明:由l与 AB交于P,且与点O,A,B不重合,
则l的斜率k:-1<k<1且k≠0,由(2)得,P(0,-k),
y1+y2=
| -2k |
| 1+2k2 |
| -k2 |
| 1+2k2 |
HA:y-1=
| y1-1 |
| x1 |
| y2+1 |
| x2 |
Q(xQ,yQ),则有
| yQ-1 |
| yQ+1 |
| y1-1 |
| y2+1 |
| x2 |
| x1 |
则
| yQ-1 |
| yQ+1 |
| yQ-1 |
| yQ+1 |
| (y1-1)2 |
| (y2+1)2 |
| x22 |
| x12 |
| 1-(y1+y2)+y1y2 |
| 1+(y1+y2)+y1y2 |
| 1+k |
| 1-k |
则有
| yQ-1 |
| yQ+1 |
| 1+k |
| 1-k |
| 1 |
| k |
则有
| OP |
| OQ |
| 1 |
| k |
| 1 |
| k |
点评:本题考查轨迹方程的求法,考查平面向量的数量积的坐标表示,考查直线方程和椭圆方程联立,运用韦达定理和弦长公式,考查直线的斜率公式的运用,以及化简整理的能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
向量
=(1,m),
=(2,-4),若
=λ
(λ为实数),则m的值为( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
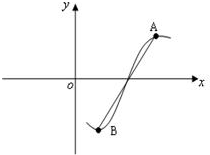 函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2
函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2