题目内容
已知点A(-2,2),B(-1,-1),若直线y=kx-2k+1与线段AB有公共点,则k的取值范围是 .
考点:恒过定点的直线
专题:直线与圆
分析:由直线方程求得直线所过定点P,然后求得PA,PB的斜率得答案.
解答:
解:由y=kx-2k+1,得y=k(x-2)+1,
∴直线y=kx-2k+1过定点P(2,1),
又A(-2,2),B(-1,-1),
如图,

∴kPA=
=-
,kPB=
=
.
∴满足直线y=kx-2k+1与线段AB有公共点的k的取值范围是[-
,
].
故答案为:[-
,
].
∴直线y=kx-2k+1过定点P(2,1),
又A(-2,2),B(-1,-1),
如图,

∴kPA=
| 2-1 |
| -2-2 |
| 1 |
| 4 |
| -1-1 |
| -1-2 |
| 2 |
| 3 |
∴满足直线y=kx-2k+1与线段AB有公共点的k的取值范围是[-
| 1 |
| 4 |
| 2 |
| 3 |
故答案为:[-
| 1 |
| 4 |
| 2 |
| 3 |
点评:本题考查了直线系方程,考查了数学结合的解题思想方法,是基础题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
有一批数量很大的产品,其中次品率为3%,从中任取产品进行不放回抽查,若取到正品则停止;若取到次品则继续,最多取3次.设X表示取出产品的个数,则P(X=3)=( )
| A、0.03×0.97 |
| B、0.972×0.03 |
| C、0.032×0.97+0.033 |
| D、0.972×0.03+0.033 |
若变量x,y满足约束条件
,且z=3x+5y,则log3
的最大值为( )
|
| z |
| 2 |
| A、18 | ||
| B、2 | ||
| C、9 | ||
D、log3
|
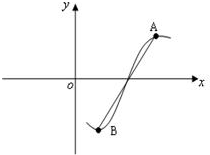 函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2
函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2