设变量x.y满足约束条件2x+y-2≥0x-2y+4≥0x-m≤0.则“m≥2 是“目标函数z=3x-2y的最大值不小于5 的( ) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

题目内容

设变量x，y满足约束条件

2x+y-2≥0

x-2y+4≥0

x-m≤0

，则“m≥2”是“目标函数z=3x-2y的最大值不小于5”的（　　）

A、充分不必要条件

B、必要不充分条件

C、充要条件

D、既不充分也不必要条件

考点：必要条件、充分条件与充要条件的判断

专题：不等式的解法及应用

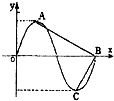
分析：作出不等式组对应的平面区域，利用充分条件和必要条件的定义进行判定．

解答： 解：作出不等式对应的可行域如图，当取点C（m，2-2m）时，z取最大值为7m-

4，
由7m-4≥5得m≥

，
故“m≥2”是“目标函数z=3x-2y的最大值不小于5”充分不必要条件，
故选A．

点评：本题主要考查充分条件和必要条件的有意义，利用线性规划的知识是解决本题的关键．

练习册系列答案

，直线l：x=6，若对于点A（m，0），存在C上的点P和l上的Q使得

sinωx（ω＞0）的部分图象如图所示，若∠ABC=90°，则函数y=f（x+1）是（　　）

执行如图所示的程序框图，若输入x=1，则输出y的值为（　　）

在△ABC中，角A，B，C的对边分别为a，b，c，且满足bsinA=

acosB．
（1）求角B的大小；
（2）求y=2sin²A+cos（

2π

-2A）取最大值时角A的大小．

试题分类