题目内容
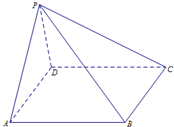 已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )
已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )A、
| ||||
B、
| ||||
| C、3 | ||||
D、3
|
考点:简单空间图形的三视图,由三视图求面积、体积
专题:空间位置关系与距离
分析:根据平面PAD⊥平面ABCD,过P作PO⊥AD,可得PO⊥平面ABCD,PO即为棱锥的高,再根据底面是边长为2的菱形,∠BAD=60°求出正视图的底边长,代入三角形面积公式计算.
解答:
解:过P作PO⊥AD,垂足为O,∵平面PAD⊥平面ABCD,PO?平面PAD,
∴PO⊥平面ABCD,
∵PA=PD=AD=2,∴PO=
,
又四棱锥的底面为边长为2的菱形,∠BAD=60°,∴AC=2
,
∴四棱锥的正视图如图:
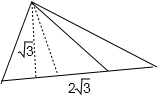
其面积S=
×2
×
=3.
故选:C.
∴PO⊥平面ABCD,
∵PA=PD=AD=2,∴PO=
| 3 |
又四棱锥的底面为边长为2的菱形,∠BAD=60°,∴AC=2
| 3 |
∴四棱锥的正视图如图:

其面积S=
| 1 |
| 2 |
| 3 |
| 3 |
故选:C.
点评:本题主要考查了三视图的面积,同时考查了面面垂直的性质,几何体的高即为正视图与侧视图的高.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
执行如图所示的程序框图,则输出的T值为( )


| A、55 | B、30 | C、91 | D、100 |
 已知函数f(x)=
已知函数f(x)=| 3 |
| A、周期为4的奇函数 |
| B、周期为4的偶函数 |
| C、周期为2π的非奇非偶函数 |
| D、周期为4的非奇非偶函数 |
已知等比数列{an},且a4+a6=π,则a5a3+2
+a5a7的值为( )
| a | 2 5 |
| A、2π |
| B、4π2 |
| C、π |
| D、π2 |
已知非零向量
,
满足|
-
|=|
+
|=λ|
|(λ≥2),则
-
与
+
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
执行如图所示的程序框图,输出的c值为( )


| A、5 | B、8 | C、13 | D、21 |