题目内容
用五点法作出函数y=2sin（2x+
），x∈[0，π]的图象
（1）根据图象，写出函数y=2sin（2x+
）在R上的单调递减区间
（2）当x∈（
，
]时，求函数的值域．
| π |
| 3 |
（1）根据图象，写出函数y=2sin（2x+
| π |
| 3 |
（2）当x∈（
| π |
| 4 |
| 3π |
| 4 |
考点：五点法作函数y=Asin（ωx+φ）的图象
专题：三角函数的求值,三角函数的图像与性质
分析：（1）分别令2x+
=0，
，π，
，2π，得到相应的x的值及y的值，再描点即可，由图可得该函数的增区间．
（2）先求得：2x+
∈（
，
]，从而可求得2sin（2x+
）∈[-2，1）．
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
（2）先求得：2x+
| π |
| 3 |
| 5π |
| 6 |
| 11π |
| 6 |
| π |
| 3 |
解答：
解：列表
图象如图：
则对应的单调增区间为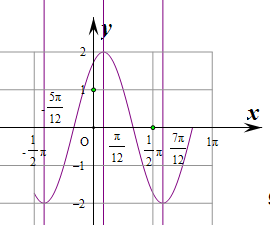
[-
+kπ，
+kπ]，减区间为[
+kπ，
+kπ]，k∈Z
（2）∵x∈（
，
]，
∴2x+
∈（
，
]，
∴2sin（2x+
）∈[-2，1）．
2x+
| 0 |
| π |
| 2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |
则对应的单调增区间为
[-| 5π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
（2）∵x∈（
| π |
| 4 |
| 3π |
| 4 |
∴2x+
| π |
| 3 |
| 5π |
| 6 |
| 11π |
| 6 |
∴2sin（2x+
| π |
| 3 |
点评：本题考查五点法作函数y=Asin（ωx+φ）的图象，着重考查余弦函数的单调性，属于中档题．
练习册系列答案
字词句段篇系列答案
相关题目
已知球的半径为2，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为2，则两圆的圆心距等于C（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |