题目内容
如果一个正方形的四个顶点都在三角形的三条边上,称该正方形是该三角形的内接正方形,若锐角△ABC的面积为S,求其内接正方形面积的最大值,并求此时正方形的边长.
考点:基本不等式
专题:不等式的解法及应用
分析:如图所示,过点A作AN⊥BC交GD于点M.设AN=h,正方形DCEF的边长CD=x,BC=a.利用平行线分线段成比例可得
=
,再利用S=
ah,可得x=
,再利用基本不等式可得x的最大值,进而得到面积的最大值.
| h-x |
| h |
| x |
| a |
| 1 |
| 2 |
| 2S | ||
h+
|
解答:
解:如图所示,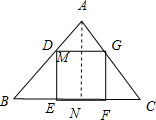
过点A作AN⊥BC交GD于点M.
设AN=h,正方形DCEF的边长CD=x,BC=a.
∵DC∥BC,则
=
,解得x=
,
而S=
ah,∴a=
,代入上式可得x=
,
∴x≤
=
,
∴正方形DCEF的面积=x2≤
S.当且仅当h=
时取等号.

过点A作AN⊥BC交GD于点M.
设AN=h,正方形DCEF的边长CD=x,BC=a.
∵DC∥BC,则
| h-x |
| h |
| x |
| a |
| ah |
| h+a |
而S=
| 1 |
| 2 |
| 2S |
| h |
| 2S | ||
h+
|
∴x≤
| 2S | ||
2
|
| ||
| 2 |
∴正方形DCEF的面积=x2≤
| 1 |
| 2 |
| 2S |
点评:本题考查了平行线分线段成比例的定理、正方形的面积、基本不等式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知ln
<ln
,若x-y<λ恒成立,则λ的取值范围是( )
| 1 |
| x+y+4 |
| 1 |
| 3x+y-2 |
| A、(-∞,10] |
| B、(-∞,10) |
| C、[10,+∞) |
| D、(10,+∞) |