题目内容
若π<α<
,化简
+
.
| 3π |
| 2 |
| 1+sinα | ||||
|
| 1-sinα | ||||
|
考点:三角函数的化简求值
专题:三角函数的求值
分析:先通分,然后利用二倍角的余弦化简,开方后去绝对值,然后在利用两角和的正弦得答案.
解答:
解:∵π<α<
,∴
<
<
,
∴
+
=
=
=
=
=
=-
.
| 3π |
| 2 |
| π |
| 2 |
| α |
| 2 |
| 3π |
| 4 |
∴
| 1+sinα | ||||
|
| 1-sinα | ||||
|
=
| 1+sinα+1-sinα | ||||
|
| 2 | ||||
|
=
| 2 | ||||||||
|
| ||||
|cos
|
| 2 | ||||
-(sin
|
| ||||
sin(
|
点评:本题考查了三角函数的化简与求值,关键是对公式的记忆与应用,是基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
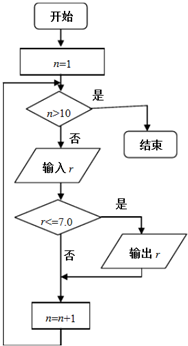 对某高中男子体育小组的50米跑成绩(单位:s)进行统计分析,得到如下的茎叶图(其中,茎表示成绩的整数部分,叶表示成绩的小数部分);
对某高中男子体育小组的50米跑成绩(单位:s)进行统计分析,得到如下的茎叶图(其中,茎表示成绩的整数部分,叶表示成绩的小数部分);