题目内容
若等比数列{an}的前n项和Sn=3n+1-m，则m的值为 ．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由等比数列的前n项和求出首项和an（n≥2），由数列是等比数列可知a1适合an=2•3n（n≥2），由此求得m的值．
解答：
解：由Sn=3n+1-m，得a1=S1=9-m；
当n≥2时，得an=Sn-Sn-1=3n+1-m-(3n-m)=2•3n．
∵数列{an}是等比数列，
∴a1=9-m适合an=2•3n（n≥2），
即9-m=2×3=6，
∴m=3．
故答案为：3．
当n≥2时，得an=Sn-Sn-1=3n+1-m-(3n-m)=2•3n．
∵数列{an}是等比数列，
∴a1=9-m适合an=2•3n（n≥2），
即9-m=2×3=6，
∴m=3．
故答案为：3．
点评：本题考查了等比数列的通项公式，考查了等比数列的前n项和，是基础题．
练习册系列答案
巧学巧练系列答案
相关题目
下列命题
①函数y=sin2x的单调增区间是[
+kπ，
+kπ]，（k∈Z）；
②函数y=tanx在（0，π）内是增函数；
③函数y=|cos2x|的最小正周期是π；
④函数y=sin（
+x）是偶函数；
其中正确的是（ ）
①函数y=sin2x的单调增区间是[
| 3π |
| 4 |
| 5π |
| 4 |
②函数y=tanx在（0，π）内是增函数；
③函数y=|cos2x|的最小正周期是π；
④函数y=sin（
| 5π |
| 2 |
其中正确的是（ ）
| A、①② | B、②③ | C、①③ | D、①④ |
若sin
=-
，cos
=-
，则角θ的终边所在象限是（ ）
| θ |
| 2 |
| 3 |
| 5 |
| θ |
| 2 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
关于“斜二测画法”，下列说法不正确的是（ ）
| A、原图形中平行于x轴的线段，其对应线段平行于x′轴，长度不变 | ||
B、原图形中平行于y轴的线段，其对应线段平行于y′轴，长度变为原来的
| ||
| C、画与直角坐标系xOy对应的x′O′y′时，∠x′O′y′必须是45° | ||
| D、在画直观图时，由于选轴的不同，所得的直观图可能不同 |
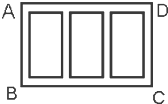如图，某广场要划定一矩形区域ABCD，并在该区域内开辟出三块形状大小相同的小矩形绿化区，这三块绿化区四周和绿化区之间均设有1米宽的走道，已知三块绿化区的总面积为200平方米，求该矩形区域ABCD占地面积的最小值．