题目内容
若“x∈[1,5]或x∈{x|x<-2或x>3}”是假命题,则x的取值范围是 .
考点:复合命题的真假
专题:简易逻辑
分析:根据已知条件即知x∉[1,5],且x∉{x|x<-2,或x>3},所以便得到
,解该不等式组即得x的取值范围.
|
解答:
解:根据已知条件,x∈[1,5],x∈{x|x<-2,或x>3}都是假命题;
∴x∉[1,5],且-2≤x≤3;
∴-2≤x<1;
∴x的取值范围是[-2,1).
故答案为:[-2,1).
∴x∉[1,5],且-2≤x≤3;
∴-2≤x<1;
∴x的取值范围是[-2,1).
故答案为:[-2,1).
点评:考查假命题的概念,p或q为假时p,q的真假情况,以及元素与集合的关系.

练习册系列答案
相关题目
与y轴相切并和圆x2+y2-10x=0外切的动圆圆心的轨迹是 ( )
| A、圆 | B、抛物线 |
| C、双曲线 | D、抛物线和一条射线 |
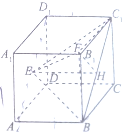 已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心.
已知正方体ABCD-A1B1C1D1棱长为1,E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心.