题目内容
设Tn为数列{an}的前n项的积,即Tn=a1•a2…•an.
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=
(1-an)(n∈N*),证明数列{
}为等差数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:
①a1•a2…•a100=2;
②a1•a2…•ak+ak+1•ak+2…a100=k+2(1≤k≤99,k∈N*).
(Ⅰ)求a5的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=
| 1 |
| 2 |
| 1 |
| Tn |
(3)数列{an}共有100项,且满足以下条件:
①a1•a2…•a100=2;
②a1•a2…•ak+ak+1•ak+2…a100=k+2(1≤k≤99,k∈N*).
(Ⅰ)求a5的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用作商法求an;
(2)利用等差数列的定义证明数列{
}为等差数列,并求得{an}的通项公式;
(3)(Ⅰ)由题意联立方程组求得T4,T5,则a5=
即得;
(Ⅱ)由(Ⅰ)可得Tk是方程x2-(k+2)x+2=0的一个实根(△>0),当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1,即得符合条件的数列共有299个.
(2)利用等差数列的定义证明数列{
| 1 |
| Tn |
(3)(Ⅰ)由题意联立方程组求得T4,T5,则a5=
| T5 |
| T4 |
(Ⅱ)由(Ⅰ)可得Tk是方程x2-(k+2)x+2=0的一个实根(△>0),当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1,即得符合条件的数列共有299个.
解答:
解:(1)当n=1时,a1=T1=1; 当n≥2时,an=
=
,
∴an=
…(4分)
(2)当n=1时,a1=T1=
(1-a1),所以a1=
,当n≥2时,2Tn=1-an=1-
,
所以
-
=2,数列{
}为等差数列 …(8分)
=3+2(n-1)=2n+1,Tn=
,an=1-2Tn=
…(10分)
(3)(Ⅰ)由a1•a2…•a100=2,a1•a2…•a4+a5•a6…a100=6;可得T4=3±
,
由a1•a2…•a100=2,a1•a2…a5+a6•a7…a100=7,可得T5=
,
所以a5=
=
或a5=
. …(13分)
(Ⅱ)a1+a2…•a100=3,所以a1=1或2
Tk是方程x2-(k+2)x+2=0的一个实根(△>0),
当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1
所以符合条件的数列共有299个.…(18分)
| Tn |
| Tn-1 |
| n2 |
| (n-1)2 |
∴an=
|
(2)当n=1时,a1=T1=
| 1 |
| 2 |
| 1 |
| 3 |
| Tn |
| Tn-1 |
所以
| 1 |
| Tn |
| 1 |
| Tn-1 |
| 1 |
| Tn |
| 1 |
| Tn |
| 1 |
| 2n+1 |
| 2n-1 |
| 2n+1 |
(3)(Ⅰ)由a1•a2…•a100=2,a1•a2…•a4+a5•a6…a100=6;可得T4=3±
| 7 |
由a1•a2…•a100=2,a1•a2…a5+a6•a7…a100=7,可得T5=
7±
| ||
| 2 |
所以a5=
| T5 |
| T4 |
7+
| ||
2(3±
|
7-
| ||
2(3±
|
(Ⅱ)a1+a2…•a100=3,所以a1=1或2
Tk是方程x2-(k+2)x+2=0的一个实根(△>0),
当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由Tk+1可得到两个ak+1
所以符合条件的数列共有299个.…(18分)
点评:本题主要考查作商法求数列通项公式及利用定义证明数列为等差数列,考查利用方程组的思想解决问题的能力,综合性强,属难题.

练习册系列答案
相关题目




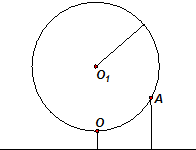 如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).
如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).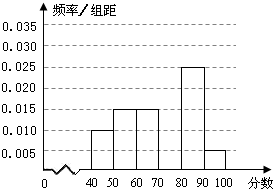 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.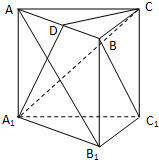 如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1. 如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么
如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么