题目内容
若函数f(x)=-x2+6x-1在区间(a,1+2a)上不是单调函数,则实数a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出函数的对称轴,结合函数的单调性,得到不等式,解出即可.
解答:
解:∵对称轴x=3,若函数在(a,1+2a)不单调,
∴a<3<1+2a,
解得:1<a<3,
故答案为:(1,3).
∴a<3<1+2a,
解得:1<a<3,
故答案为:(1,3).
点评:本题考查了二次函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(0,3) |
| B、(0,3] |
| C、(3,+∞) |
| D、[3,+∞) |
设x、y满足约束条件
,若x+2y≤a能成立,则a的取值范围为( )
|
| A、(-∞,1] |
| B、[1,+∞) |
| C、(-∞,7] |
| D、[7,+∞) |
在△ABC中,∠A,∠B,∠C所对的边为a,b,c,a=8,B=60°,A=45°,则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|
已知点A在球O的表面上,过点A的作平面α,使OA与平面α成30°角,若平面α截球所得的圆面积为3π,则球O的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、16π |
某几何体的三视图如图所示,则该几何体的体积为( )
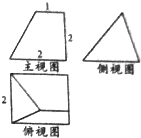

| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
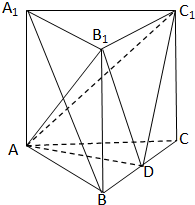 如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点