题目内容
设函数f(x)=
,g(x)=
,若f[g(a)]≤1,则实数a的取值范围是 .
|
| 2 |
| x |
考点:分段函数的应用
专题:函数的性质及应用
分析:先考虑g(a)=
,则f[g(a)]=f(
),故f[g(a)]≤1?f(
)≤1,
当
≤0时,f(
)=(2)
;当
>0时,f(
)=log2(
),化为指数不等式与对数不等式即可求出a的范围.注意最后求交集.
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
当
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
解答:
解:g(a)=
,∴f[g(a)]=f(
),∴f[g(a)]≤1?f(
)≤1,
当
≤0时,f(
)=(2)
;当
>0时,f(
)=log2(
)
∴不等式可化为
或
,
解此不等式组得a<0\,或a≥2,
故答案为:(-∞,0)∪[2,+∞).
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
当
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
∴不等式可化为
|
|
解此不等式组得a<0\,或a≥2,
故答案为:(-∞,0)∪[2,+∞).
点评:本题考查分段函数和运用,考查对数函数的单调性和应用,考查不等式的恒成立问题,运用参数分离法,求最值,属于中档题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
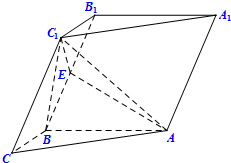 如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=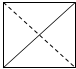 在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
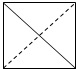
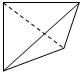
在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.