题目内容
9.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,0≤x≤$\frac{1}{2}$≤y≤1,则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$|的最小值为$\frac{1}{4}$.分析 单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,不妨设$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$=x($\overrightarrow{a}-\overrightarrow{c}$)+y$(\overrightarrow{b}-\overrightarrow{c}$)+$\overrightarrow{c}$=(-$\frac{3}{2}x+\frac{1}{2}$,$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$),
则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$|2=(-$\frac{3}{2}$x+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$)2,再利用柯西不等式求解.
解答  解:单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,不妨设$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)(如图),
解:单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,不妨设$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)(如图),
x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$=x($\overrightarrow{a}-\overrightarrow{c}$)+y$(\overrightarrow{b}-\overrightarrow{c}$)+$\overrightarrow{c}$=(-$\frac{3}{2}x+\frac{1}{2}$,$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$),
∴|x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$|2=(-$\frac{3}{2}$x+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$)2,
由柯西不等式得=[(-$\frac{3}{2}$x+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$)2]•[($\sqrt{3}$)2+32]≥[$\sqrt{3}$(-$\frac{3}{2}x+\frac{1}{2}$)+3($\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$)]2=(3$\sqrt{3}$y-$\sqrt{3}$)2
∵$\frac{1}{2}$≤y≤1,∴y=$\frac{1}{2}$时,(-$\frac{3}{2}$x+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$)2最小为$\frac{1}{16}$
则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+(1-x-y)$\overrightarrow{c}$|的最小值为$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了向量的模的取值范围的求法,考查了不等式的性质,转化思想,属于中档题.


| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{n}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{n}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{n}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(1)根据散点图判断,$y=a+bx,y=c+d\sqrt{x}$哪一个更适合作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据(2)的结果回答下列问题;
①当年宣传费x=90时,年销售量及年利润的预报值是多少?
②当年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:
$\widehat{β}$=$\frac{\sum_{i=1}^{n}({μ}_{i}-\overline{μ})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({μ}_{i}-\overline{μ})^{2}}$,$\widehat{a}$=$\overline{v}$-$\widehat{β}$$\overline{μ}$.
| 特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
| y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程$\widehaty=\widehatbt+\widehata$中斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.${\sum_{i=1}^7{({{t_i}-\overline t})}^2}=432$.
| x | 3 | 4 | 5 | 6 |
| y | 25 | 30 | 40 | 45 |
附:$\widehat{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)•({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$;$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| A. | 59.5 | B. | 52.5 | C. | 56 | D. | 63.5 |
| A. | {4} | B. | {5} | C. | [4,5] | D. | {4,5} |
 如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.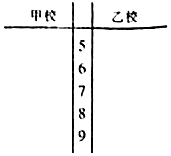 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下: