题目内容
14．现从某班的一次期末考试中，随机的抽取了七位同学的数学（满分150分）、物理（满分110分）成绩如表所示，数学、物理成绩分别用特征量t，y表示，| 特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
| y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩（精确到个位）．
附：回归方程$\widehaty=\widehatbt+\widehata$中斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．${\sum_{i=1}^7{（{{t_i}-\overline t}）}^2}=432$．
分析 （1）求出样本中心坐标，代入回归直线方程，然后求解回归直线方程．
（2）利用回归直线方程判断分析数学成绩的变化对物理成绩的影响，然后求解物理成绩．
解答 解：（1）∵$\overline t=\frac{101+124+119+106+122+118+115}{7}=115$．…（2分）
$\overline y=\frac{74+83+87+75+85+87+83}{7}=82$．…．（4分）
设回归方程为$\widehaty=\widehatbt+\widehata$，代入公式，经计算得$\widehatb=\frac{14×8+9×1+4×5+9×7+7×3+3×5+0×1}{196+81+16+81+49+9}=\frac{240}{432}=\frac{5}{9}$…（6分）$\widehata=\overline y-\widehatb\overline t=82-\frac{5}{9}×115=\frac{163}{9}$，∴y关于t的回归方程为$\widehaty=\frac{5}{9}t+\frac{163}{9}$…．（8分）
（2）∵$\widehatb=\frac{5}{9}＞0$，∴随着数学成绩的提高，物理成绩会稳步增长，…..（9分）
当t=130时，$y=\frac{5}{9}×130+\frac{163}{9}=\frac{271}{3}≈90$．
所以，该班某学生数学成绩130（分）时，他的物理成绩估计为90（分）…..（12分）
点评 本题考查回归直线方程的求法与应用，考查计算能力．
练习册系列答案
相关题目
19．第96届（春季）全国糖酒商品交易会于2017年3月23日至25日在四川举办．交易会开始前，展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系，查阅了最近5次交易会的参会人数x（万人）与餐厅所用原材料数量t（袋），得到如下数据：
（Ⅰ）请根据所给五组数据，求出t关于x的线性回归方程$\hat t=\hat bx+\hat a$；
（Ⅱ）已知购买原材料的费用C（元）与数量t（袋）的关系为$C=\left\{\begin{array}{l}300t+20，（{0＜t＜35，t∈N}）\\ 290t，（{t≥35，t∈N}）\end{array}\right.$投入使用的每袋原材料相应的销售收入为600元，多余的原材料只能无偿返还．若餐厅原材料现恰好用完，据悉本次交易会大约有14万人参加，根据（Ⅰ）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润L=销售收入-原材料费用）．
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$）
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x（万人） | 11 | 9 | 8 | 10 | 12 |
| 原材料t（袋） | 28 | 23 | 20 | 25 | 29 |
（Ⅱ）已知购买原材料的费用C（元）与数量t（袋）的关系为$C=\left\{\begin{array}{l}300t+20，（{0＜t＜35，t∈N}）\\ 290t，（{t≥35，t∈N}）\end{array}\right.$投入使用的每袋原材料相应的销售收入为600元，多余的原材料只能无偿返还．若餐厅原材料现恰好用完，据悉本次交易会大约有14万人参加，根据（Ⅰ）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润L=销售收入-原材料费用）．
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$）
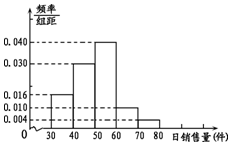某超市计划销售某种产品，先试销该产品n天，对这n天日销售量进行统计，得到频率分布直方图如图．