题目内容
10. 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=$\sqrt{6}$,AC=CD=2,DE=BE=1.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=$\sqrt{6}$,AC=CD=2,DE=BE=1.(1)证明:DE⊥平面ACD;
(2)求二面角B-AD-E的余弦值.
分析 (1)依题意,易证AC⊥平面BCDE,于是可得AC⊥DE,又DE⊥DC,从而DE⊥平面ACD
(2)以D为原点,分别以DE,DC为x,y轴的正半轴,与CA平行的直线为z轴,求出平面ADE、平面ADB的法向量即可,
解答 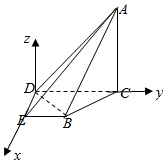 证明:(1)在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=$\sqrt{2}$,
证明:(1)在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=$\sqrt{2}$,
由AC=2,AB=$\sqrt{6}$,得AB2=AC2+BC2,即AC⊥BC,
又平面ABC⊥平面BCDE,从而AC⊥平面BCDE,
所以AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;
(2)解:由(1)得AC⊥平面BCDE,以D为原点,
分别以DE,DC为x,y轴的正半轴,与CA平行的直线为z轴,
如图,D(0,0,0),E(1,0,0),A(0,2,2),B(1,1,0),
$\overrightarrow{DA}=(0,2,2)$,$\overrightarrow{DB}=(1,1,0)$,$\overrightarrow{DE}=(1,0,0)$.
设平面ADE的法向量为$\overrightarrow{m}$=(x1,y1,z1),由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DA}=2{y}_{1}+2{z}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{DE}={x}_{1}=0}\end{array}\right.$
可取$\overrightarrow{m}=(0,1,-1$).
设平面ABD的法向量为$\overrightarrow{n}$=(x2,y2,z2),由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DA}=2{y}_{2}+2{z}_{2}=0}\\{\overrightarrow{n}•\overrightarrow{DB}={x}_{2}+{y}_{2}=0}\end{array}\right.$,
可取$\overrightarrow{n}=(1,-1,1)$,
∴cos $<\overrightarrow{n},\overrightarrow{m}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-2}{\sqrt{2}×\sqrt{3}}$=-$\frac{\sqrt{6}}{3}$
∴二面角B-AD-E的余弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查了空间位置关系、空间角、法向量的应用、向量垂直与数量积的关系、勾股定理与逆定理、余弦定理,考查了推理能力与计算能力,属于中档题.

 黄冈创优卷系列答案
黄冈创优卷系列答案| A. | $\frac{7\sqrt{2}}{8}$ | B. | $\frac{5\sqrt{2}}{4}$ | C. | $\frac{7\sqrt{3}}{8}$ | D. | $\frac{5\sqrt{3}}{4}$ |
| A. | f(cosA)>f(sinB) | B. | f(sinA)>f(cosB) | C. | f(cosA)≥f(sinB) | D. | f(sinA)≥f(cosB) |
| A. | 8° | B. | 44° | C. | 40° | D. | 80° |
| A. | C${\;}_{2017}^{40}$ | B. | C${\;}_{2017}^{41}$ | C. | A${\;}_{2017}^{40}$ | D. | A${\;}_{2017}^{41}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 与离家的直线距离
与离家的直线距离 之间的函数图象(如下图).若用黑点表示唐校长家的位置,则唐校长晨练所走的路线可能是( )
之间的函数图象(如下图).若用黑点表示唐校长家的位置,则唐校长晨练所走的路线可能是( )

 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD.当∠ABC=45°时,对角线BD的长为$\sqrt{7}$.