题目内容
由xy=4，x=1，x=4，y=0围成的平面区域绕x轴旋转所得的旋转体的体积是 ．
考点：用定积分求简单几何体的体积
专题：导数的综合应用
分析：由曲线y=x3及直线y=1，x=0围成的区域绕x轴旋转一周得到的旋转体体积V=π本题考查旋转体体积的求法，是中档题，解题时要认真审题，注意定积分的合理运用．
解答：
解：由xy=4，x=1，x=4，y=0围成的区域绕x轴旋转一周得到的旋转体体积：V=
(
)2dx=16π（-
）|
=12π．
故答案为：12π．
| π∫ | 4 1 |
| 4 |
| x |
| 1 |
| x |
4 1 |
故答案为：12π．
点评：本题考查利用定积分求不规则旋转体体积的求法，是中档题，解题时要认真审题，注意定积分的合理运用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
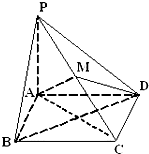如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=1，点M是棱PC上的一点，且AM⊥PB．
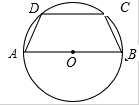四边形ABCD是⊙O的内接等腰梯形，AB为直径，且AB=4．设∠BOC=θ，ABCD的周长为L．