题目内容
已知函数f(x)=(1-x)ex-1.
(1)证明:当x>0时,f(x)<0;
(2)设数列{xn}满足xnexn+1=exn-1且x1=1,证明:{xn}单调递减且xn>
.
(1)证明:当x>0时,f(x)<0;
(2)设数列{xn}满足xnexn+1=exn-1且x1=1,证明:{xn}单调递减且xn>
| 1 |
| 2n |
考点:数列与函数的综合,利用导数研究函数的极值
专题:综合题,等差数列与等比数列
分析:(1)求导数,确定函数的单调性,即可证明当x>0时,f(x)<0;
(2)首先用数学归纳法证明xn>
,再结合exn-1<xnexn,即可证明:{xn}单调递减.
(2)首先用数学归纳法证明xn>
| 1 |
| 2n |
解答:
证明:(1)因为f(x)=(1-x)ex-1,
所以f′(x)=-ex+(1-x)ex=-xex,
当x>0时,f′(x)<0,所以函数f(x)在(0,+∞)上单调递减,
因此f(x)<f(0)=0. …2分
(2)首先用数学归纳法证明xn>
.
①当n=1时,11=1>
,所以x1>
成立.
②假设n=k时,xk>
.
那么当n=k+1时,xnexn+1=exn-1,则exk+1=
,…4分
当x>0时,由不等式ex-1>x得
>1且g(x)=
在(0,+∞)单调递增,
∵xk>
,
∴exk+1=
>
>
.
所以xk+1>
.
由①②可知对任意的正整数n,总有xn>
.
由(1)知(1-xn)exn-1<0,所以exn-1<xnexn.
由xnexn+1=exn-1知xn+1<xn.
所以{xn}单调递减 …10分.
所以f′(x)=-ex+(1-x)ex=-xex,
当x>0时,f′(x)<0,所以函数f(x)在(0,+∞)上单调递减,
因此f(x)<f(0)=0. …2分
(2)首先用数学归纳法证明xn>
| 1 |
| 2n |
①当n=1时,11=1>
| 1 |
| 2 |
| 1 |
| 2 |
②假设n=k时,xk>
| 1 |
| 2k |
那么当n=k+1时,xnexn+1=exn-1,则exk+1=
| exk-1 |
| xk |
当x>0时,由不等式ex-1>x得
| ex-1 |
| x |
| ex-1 |
| x |
∵xk>
| 1 |
| 2k |
∴exk+1=
| exk-1 |
| xk |
e
| ||
|
| 1 |
| 2k+1 |
所以xk+1>
| 1 |
| 2k+1 |
由①②可知对任意的正整数n,总有xn>
| 1 |
| 2n |
由(1)知(1-xn)exn-1<0,所以exn-1<xnexn.
由xnexn+1=exn-1知xn+1<xn.
所以{xn}单调递减 …10分.
点评:本题考查导数知识的运用,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
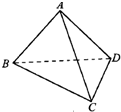 如图四面体ABCD的棱BD长为2,其余各棱长均为
如图四面体ABCD的棱BD长为2,其余各棱长均为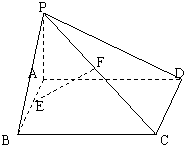 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.