题目内容
已知锐角三角形ABC的外接圆的圆心为O,半径为R,已知∠A=30°且
cosB+
cosC=
,则m=( )
| ||
| |AB| |
| ||
| |AC| |
| m |
| R |
| AO |
A、-
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:平面向量数量积的含义与物理意义
专题:计算题,平面向量及应用
分析:由
cosB+
cosC=
,两边同时乘向量
,结合正弦定理化边为角即可求得m值.
| ||
| |AB| |
| ||
| |AC| |
| m |
| R |
| AO |
| OA |
解答:
解:由
cosB+
cosC=
,
两边同时乘向量
,得
(
•
-
2)+
(
•
-
2)=-
•R2,
所以
(-2sin2C)+
(-2sin2B)=-
,
由正弦定理可得-2sinCcosB-2sinBcosC=-2m,即2sin(B+C)=2m,
因为∠A=30°,所以m=
.
故选:D.
| ||
| |AB| |
| ||
| |AC| |
| m |
| R |
| AO |
两边同时乘向量
| OA |
| cosB |
| c |
| OB |
| OA |
| OA |
| cosC |
| b |
| OC |
| OA |
| OA |
| m |
| R |
所以
| cosB |
| c |
| cosC |
| b |
| m |
| R |
由正弦定理可得-2sinCcosB-2sinBcosC=-2m,即2sin(B+C)=2m,
因为∠A=30°,所以m=
| 1 |
| 2 |
故选:D.
点评:本题考查平面向量的基本定理、向量数量积运算、正弦定理等知识,本题解答的关键是两边同乘向量
,具有一定技巧.
| OA |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知平面α,β所成的二面角为80°,P为α,β外一定点,则过点P作直线与α,β都成30°的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
复数1-2i(i是虚数单位)的虚部是( )
| A、2i | B、-2i | C、2 | D、-2 |
已知点A(2,4),B(3,6),则直线AB的斜率是( )
| A、1 | B、2 | C、3 | D、4 |
过点(-1,3)且平行于直线x-2y+3=0的直线方程为( )
| A、x-2y=0 |
| B、2x+y-1=0 |
| C、x-2y+7=0 |
| D、2x+y-5=0 |
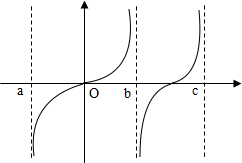 已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断:
已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断: