题目内容
19.B是单位圆O上的点,点A(1,0),点B在第二象限.记∠AOB=θ且sinθ=$\frac{4}{5}$.(1)求B点坐标;
(2)求$\frac{sin(π+θ)+2sin(\frac{π}{2}-θ)}{2cos(π-θ)}$的值.
分析 (1)由已知条件设出B点坐标为(x,y),即可求出y和x的值,则B点坐标可求;
(2)利用三角函数的诱导公式化简代值计算即可得答案.
解答 解:(1)∵点A是单位圆与x轴正半轴的交点,点B在第二象限.
设B点坐标为(x,y),则y=sinθ=$\frac{4}{5}$.$x=-\frac{3}{5}$,即B点坐标为:$(-\frac{3}{5},\frac{4}{5})$;
(2)$\frac{{sin(π+θ)+2sin(\frac{π}{2}-θ)}}{2cos(π-θ)}=\frac{-sinθ+2cosθ}{-2cosθ}=\frac{{-\frac{4}{5}-\frac{6}{5}}}{{\frac{6}{5}}}=-\frac{5}{3}$.
点评 本题考查了三角函数的化简求值,考查了三角函数的诱导公式的应用,是基础题.

练习册系列答案
相关题目
10.当下面的程序段输出结果是41,则横线处应填( )


| A. | i>4 | B. | i>=4 | C. | i<4 | D. | i<=4 |
14.已知点M(5,-6)和向量$\overrightarrow{a}$=(1,-2),若$\overrightarrow{NM}$=3$\overrightarrow{a}$,则点N的坐标为( )
| A. | (2,0) | B. | (-3,6) | C. | (6,2) | D. | (-2,0) |
4.已知变量x,y满足$\left\{{\begin{array}{l}{x+2y-4≤0}\\{x≥1}\\{y≥0}\end{array}}\right.$,则z=-2x+y的最大值是( )
| A. | 2 | B. | $-\frac{1}{2}$ | C. | -2 | D. | -8 |
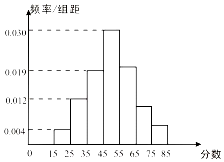 某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.