设函数f(x)=$\left\{\begin{array}{l}{lo{g} {2}x.x＞0}\\{-x.x＜0}\end{array}\right.$.则fA．1B．2C．$-\frac{1}{2}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

18．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{-x，x＜0}\end{array}\right.$，则f（f（-2））等于（　　）

A．

B．

C．

$-\frac{1}{2}$

D．

$\frac{1}{2}$

分析由函数性质得f（-2）=-（-2）=2，从而f（f（-2））=f（2），由此能求出结果．

解答解：∵函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{-x，x＜0}\end{array}\right.$，
∴f（-2）=-（-2）=2，
f（f（-2））=f（2）=log₂2=1．
故选：A．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案

小学毕业升学复习必做的18套试卷系列答案

$\frac{{3\sqrt{15}}}{8}$

9．与圆（x-2）²+（y+1）²=4外切于点A（4，-1）且半径为1的圆的方程为（x-5）2+（y+1）2=1．

6．5人排成一列，其中甲、乙二人相邻的不同排法的种数为48．（结果用数字表示）

13．设集合A={1，2，3}，B={1，2，3}，分别从集合A和B中随机取一个数a和b，确定平面上的一个点P（a，b），记“点P（a，b）落在直线x+y=n上”为事件C_n（2≤n≤6，n∈N），若事件C_n的概率最大，则n的所有可能值为（　　）

3．根据下列条件，求直线方程：
（1）过点（2，1）且与直线y=x平行；
（2）过点（1，5），且与直线y=2x垂直．

10．当下面的程序段输出结果是41，则横线处应填（　　）

7．已知角α的终边过点（3，4）．
（Ⅰ）求sinα，cosα的值；
（Ⅱ）求$\frac{{2cos（{\frac{π}{2}-α}）-cos（{π+α}）}}{{2sin（{π-α}）}}$的值．

8．

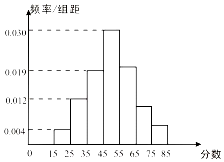某校1400名学生参加某次知识竞赛，从中随机抽取100名考生的成绩，绘制成如图所示的频率分布直方图，分数落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
（1）求这些分数落在区间[55，65）内的频率；
（2）估计该校参加本次知识竞赛中成绩低于45分的人数是多少？

试题分类