题目内容
3.设a>0,b>0,若a+b=1,则$\frac{1}{a}+\frac{1}{b}$的最小值是( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵a>0,b>0,a+b=1,
则$\frac{1}{a}+\frac{1}{b}$=(a+b)$(\frac{1}{a}+\frac{1}{b})$=2+$\frac{b}{a}+\frac{a}{b}$$≥2+2\sqrt{\frac{b}{a}•\frac{a}{b}}$=4,当且仅当a=b=$\frac{1}{2}$时取等号.
∴其最小值是4.
故选:C.
点评 本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
13.设集合A={1,2,3},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤6,n∈N),若事件Cn的概率最大,则n的所有可能值为( )
| A. | 4 | B. | 2和6 | C. | 3和5 | D. | 3 |
14.已知点M(5,-6)和向量$\overrightarrow{a}$=(1,-2),若$\overrightarrow{NM}$=3$\overrightarrow{a}$,则点N的坐标为( )
| A. | (2,0) | B. | (-3,6) | C. | (6,2) | D. | (-2,0) |
18.阅读如图所示的程序框图,运行相应的程序,输出的S的值等于( )


| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
15.设函数f(x)=ax+bx+cx,其中c>a>0,c>b>0,若a,b,c是△ABC的三条边长,则下列结论正确的是( )
①对任意x∈(-∞,1),都有f(x)<0;
②存在x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,存在x∈(1,2),使f(x)=0.
①对任意x∈(-∞,1),都有f(x)<0;
②存在x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,存在x∈(1,2),使f(x)=0.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
13.设Sn是等差数列{an}的前项和,若S4≠0,且S8=3S4,设S12=λS8,则λ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
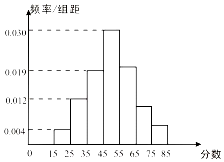 某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.