题目内容
10.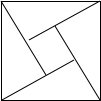 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4-\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 根据几何概率的求法:一次飞镖扎在中间小正方形区域(含边线)的概率就是阴影区域的面积与总面积的比值.
解答 解:观察这个图可知:大正方形的边长为2,总面积为4,
而阴影区域的边长为$\sqrt{3}$-1,面积为4-2$\sqrt{3}$;
故飞镖落在阴影区域的概率 $\frac{4-2\sqrt{3}}{4}$=1-$\frac{\sqrt{3}}{2}$;
故选:A.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率;关键是得到两个正方形的边长.

练习册系列答案
相关题目
18.已知2sinx=1+cosx,则$cot\frac{x}{2}$=( )
| A. | 2 | B. | 2或$\frac{1}{2}$ | C. | 2或0 | D. | $\frac{1}{2}$或0 |
5.毛泽东同志在《清平乐•六盘山》中的两句诗为“不到长城非好汉,屈指行程二万”,假设诗句的前一句为真命题,则“到长城”是“好汉”的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.若集合M={1,3},N={1,3,5},则满足M∪X=N的集合X的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.若抛物线y2=2px(p>0)的焦点与双曲线$\frac{{x}^{2}}{3}$-y2=1的一个焦点重合,则p=( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
13.已知点P(4,-3)在角φ的终边上,函数f(x)=sin(ωx+φ)(ω>0)图象上与y轴最近的两个对称中心间的距离为$\frac{π}{2}$,则f($\frac{π}{8}$)的值为( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{7\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |